РАЗДЕЛ IV. ФИЛОСОФИЯ ПРЕДЛОЖЕНИЯ

Глава 1. Ян Лукасевич и Варшавская школа логики.

§ 1. Метафизические основания логического анализа.

Если о Лесьневском было сказано, что он является метафизиком в логике, то про Я. Лукасевича можно утверждать обратное - что он логик в метафизике. Связь этих двух областей философского знания применительно к творчеству Лукасевича состоит в том, что его продвижение по логическому пути было инспирировано вопросами метафизики, или более широко - онтологии. Чтобы это показать обратимся к принятому выше делению суждений на номинальные и реальные и установим к какому из упомянутых типов суждений тяготел в своем творчестве Лукасевич. По поводу номинального суждения можно сказать, что оно не занимало Лукасевича, ибо в его работах понятие имени не анализируется. Остается предположить, что точкой приложения анализа окажется реальное суждение, составляющее предмет парадигмы философии предложения. Показателем этой парадигмы в анализе суждения является опосредованное непрямым использованием имя суждения, т.е. истинностное значение. Но истинность суждения как таковая не имеет ценности, ибо " [...] сама по себе истинность не является достаточным свойством научных предложений, [...] истинные предложения приобретают научную ценность лишь тогда, когда остаются в некой связи с интеллектуальными потребностями человека". Более того, "истина не только не достаточна, но даже не является необходимым свойством научных предложений" ([1915], S.81]). Приведенные высказывания можно объяснить тем, что по мнению Лукасевича интеллектуальные потребности может удовлетворить только теория. Однако "ни одна теория не является чистым воспроизведением фактов, но каждая содержит творческий элемент. Поэтому и истинность ни одной теории не удается доказать, если мы понимаем истинность как согласие мышления с действительностью". ( S. 81)

Таким образом, истина должна быть научной, что следует понимать как истинность предложений теории, т.е. истинность становится относительной и, наконец, истинность не самодостаточна, а служит выявлению причин и следствий из фактов. Следовательно и реальное суждение, как и его косвенно употребляемое имя - истинностное значение не является для Лукасевича предметом анализа, но таковыми становится в начальном, т.е. философском периоде его творчества предметы метафизические, в частности понятие причины, рассмотрению которого посвящена работа "Анализ и конструкция понятия причины". В ней он пишет: "Конструируя понятие причины, я намерен создать некий абстрактный предмет с той целью, чтобы он охватывал все конкретные и реальные причины, существование которых мы принимаем то ли во внешнем мире, то ли в мире явлений духа; однако я не веду речь о некотором идеальном предмете, которому бы в действительности, как четырехмерной глыбе, ничто не может соответствовать. Тогда, если я понимаю причину как некий реальный абстрактный предмет, то стремясь его создать, я могу использовать только один путь - индуктивный метод." ([1906], S.15) Весь путь Лукасевича от философии к логике может быть очерчен в методе как путь от индукции к дедукции, о чем косвенно свидетельствуют названия его работ начального периода: "Об индукции как инверсии дедукции" [1903], "О двух видах индуктивного следования"[1906], "Об индуктивном следовании"[1907].

Приступая к изложению философских работ Лукасевича можно утверждать, что они сформировали его логические взгляды не только в методе, но и в предмете. Отыскание такого предмета в парадигме философии предложения весьма затруднительно, т.к. в этом случае предложению, являющемуся этим предметом, следует поставить в соответствие имя в функции употребления, а не упоминания, что непросто, т.к. и закавыченное предложение, и истинностное значение упоминаются, а не употребляются. На вопрос: что является предметом философии Лукасевича и как он был отражен в более позднем, или логическом периоде его творчества - на этот вопрос получить ответ еще предстоит, невзирая на отступнические заверения, подобные ранее приведенным высказываниям Лесьневского. Одно из таких высказываний Лукасевича, сделанных им в логическом периоде, таково: "Я пришел в логистику из философии и логистика, в действительности не из-за своего содержания, но с точки зрения своего метода, оказала огромное влияние на мое мнение о философии [...]. Моя критическая оценка философии того времени является реакцией человека, который изучивши философию и начитавшись досыта различных философских книжек наконец столкнулся с научным методом не только в теории, но и в живой личной практике творчества". ([1936], S.202)

Философские взгляды Лукасевича реконструируем на основе уже упоминавшейся работы о понятии причины [1906]. Рассматривая главный вопрос этой работы, т.е. анализ и конструкцию понятия причины Лукасевич предваряет его рядом замечаний о понятии самого понятия. Считая понятие абстрактным предметом он признается, что не умеет его определить. Однако можно сказать, чем понятия не являются; они не являются психическими процессами или же какими-то образами, находящимися в сознании. Понятия суть вневременные и внепространственные объекты и такой платоновский взгляд на сущность понятий Лукасевич считает единственно верным. Абстрактные предметы могут быть либо идеальными, либо реальными. Первыми занимается математика и логика. Создание идеальных предметов человеческим мышлением независимо от того, существуют ли они в действительном мире. Реальные абстрактные предметы - это те, о которых говорят естествоиспытатели; ведь они говорят не только, например, об ускорении некоторого конкретного объекта, но об ускорении вообще. Тем не менее реальные абстрактные предметы, в отличие от идеальных, создаются с намерением отражения некоторых конкретных вещей. Любое абстрактное понятие, если оно используется в науке, должно быть непротиворечиво. Для "значимости" идеальных предметов непротиворечивость достаточна. Но для реальных абстрактных предметов непротиворечивость является только необходимым условием их "значимости". Чтобы эти предметы использовались в науке они должны обладать такими свойствами, которые мы находим в соответствующих конкретных предметах.

Под логическим анализом понятия Лукасевич понимает обнаружение свойств этого понятия и отношений, возникающих между свойствами. Логический анализ придает особое значение необходимым отношениям, что ведет к выявлению совокупности существенных свойств и несущественных, случайных. После проведения логического анализа, считает Лукасевич, можно заняться конструкцией данного понятия. Логический анализ требует использования определенных методов и различия между идеальными и реальными (абстрактными) предметами приводят к тому, что методы анализа (и конструкции) обоих видов понятий должны быть различны. В частности, анализ и конструкция идеального понятия не должны опираться на опыт. Как кажется, - хотя Лукасевич об этом и не говорит прямо, - анализ идеальных понятий заключается в дедуктивном нахождении следствий из предпосылок, выражающих существенные свойства понятия, тогда как исследование реальных понятий требует использования метода, который Лукасевич называет индуктивным. Он состоит в рассмотрении примеров конкретных объектов, подпадающих под исследуемое реальное понятие. Целью индуктивного исследования является обнаружение общих, характерных свойств объекта. Применение индуктивного метода служит начальным шагом, предоставляющим материал для дальнейшего исследования методом дедуктивным. Дедукция, являющаяся вторым шагом в исследовании понятий, позволяет определить существенные свойства, или, как их называет Лукасевич, конституирующие, она позволяет обнаружить отношения между этими свойствами, изучить вопрос согласованности свойств. По мнению Лукасевича анализ должен привести к конструкции непротиворечивого, однозначного и согласованного с действительностью (в случае реальных понятий), а потому и научного понятия.

Так очерченный аналитический метод Лукасевич применяет к анализу и конструкции понятия причины. Поскольку это понятие является реальным абстрактным предметом, то согласно ранее сделанным допущениям, оно должно исследоваться индуктивным и дедуктивным методом. Некоторые шаги анализа Лукасевича выглядят следующим образом. Так индукция подсказывает, что следствие и причина соотносительны. Из этого он заключает, что каждая причина имеет какое-либо следствие, а каждое следствие - некоторую причину. Однако последнее утверждение следует отличать от тезиса, будто бы каждое явление имеет свою причину; этот тезис являет собой т.н. принцип причинности, который сам по себе не определен и требует обоснования. Лукасевич критикует также взгляд, будто сущность причинной связи заключена в действии причины на следствие. Такой взгляд он считает неправильным, поскольку можно без противоречия утверждать, что существует действующая субстанция, но нет следствия этого воздействия, но утверждать непротиворечиво (ввиду соотносительности причины и следствия), что есть причина и не существует ее следствие - невозможно. Таким образом, причина не может быть отождествлена с действующей субстанцией. Логический анализ также подсказывает ошибочность взгляда Юма-Милля, согласно которому отношение причинности состоит в постоянной связи событий, поскольку легко показать, что эти два отношения пересекаются. По мнению Лукасевича фактором, формирующим отношение причинности, является некоторое необходимое отношение. Лукасевич вполне сознает, что в этом пункте он касается весьма тонкого вопроса, отмеченного Юмом: необходимость причинной связи может не быть обнаружена в опыте. Однако из того, что некоторое свойство не обнаруживается в опыте не следует, что предметы опыта не обладают этим свойством. Чтобы сделать правдоподобным, будто отношению причинности свойственна необходимость, достаточно в опыте убедиться, что данная причина в каждом рассматриваемом случае вызывает данное следствие, и что отсутствие данного следствия в каждом случае связано с отсутствием данной причины и имеют место случаи появления данного следствия без появления причины. Если мы в этом убедимся, то правомерно утверждать, что между отношением причинности и логическим отношением основания и следствия имеет место аналогия, т.е. аналогия с отношением, которое несомненно необходимо. Лукасевич считает, что опыт позволяет выдвигать выше приведенную аналогию. Однако ее недостаточно для редукции отношения причинности к логическому отношению основания и следствия, поскольку онтологическая природа членов обоих отношений различна. И тем не менее логическая необходимость, считает Лукасевич, является производной от необходимости онтологической. В конечном счете причинность является необходимым онтологическим отношением со свойствами, аналогичными свойствам логического отношения между основанием и следствием. В частности эта аналогия позволяет установить, что отношение причинности несимметрично и транзитивно.

Здесь необходимо отметить, что по мнению Лукасевича методы анализа и конструирования могут привести к научной метафизике, которую он отождествлял с общей теорией предметов в брентанистском понимании, и в этом смысле влияние Твардовского на Лукасевича очевидно. Так понимаемую метафизику, близкую к мейнонговской трактовке, Лукасевич был склонен считать фундаментом философии; его взгляды в этом вопросе отличались от взглядов Твардовского, для которого таким фундаментом была дескриптивная психология, т.е. de facto гносеология. Лукасевич же считал, что гносеологическая точка зрения в философии в конечном счете приводит к психологизму, в котором он обвинял не только австрийскую философию, в среде которой сформировались его взгляды, но и вообще философию Нового времени: "Мои взгляды возникли из противостояния великим системам современной философии, например, Юма или Канта. [...] Когда я мысленно пробегаю свершения современной философии с того времени, когда Декарт хотел воздвигнуть на новых основаниях все человеческое познание и обосновал свое известное "cogito, ergo sum", а также сформулировал понятие "clarae et distinctae perceptionis", с того времени, когда Локк однажды вечером после неудачной метафизической дискуссии пришел к мысли исследовать источники уверенности и границы человеческого познания, а Юм и Кант, подхватив эту мысль, сделали ноэтические исследования осью своей философии, тогда я не могу противиться убеждению, что все это психологическое направление философской мысли приводит ее на бездорожье."[1907, S.53]

Психологизм был популярен в XIX ст. Несколько огрублено, он состоял в том, что провозглашал существование некоторых предметов в психике, в частности таких “неудобных” как понятия, суждения, числа, произведения искусств, законы и т.п. Познание этих предметов заключалось в познании неких психических актов, а психология таким образом становилась основой ряда наук. Психологизм был доминирующим течением до конца XIX ст. покамест в начале XX ст. в результате критики неокантианцев, подвергших сомнению психологическую интерпретацию своего учителя, он не уступил, сначала апсихологизму, а потом антипсихологизму, подготовившему почву эмпиризма для неопозитивистских претензий. Не в последнюю очередь психологизм был изжит также трудами Г.Фреге и Э.Гуссерля.

В начальном периоде Львовско-варшавская школа, продолжившая традиции брентанизма, находилась под влиянием психологизма. Первым, кто в этом интеллектуальном содружестве восстал против психологизма, был Я.Лукасевич. Его критика в работе “Логика и психология” [1907] относилась к психологизму, понимаемому как редукция логики к психологии. Сформулированные Лукасевичем аргументы против психологизма сводились к следующим положениям: а) психологические суждения, являясь всего лишь правдоподобными, не могут служить основанием для логических суждений, которые достоверны, поскольку достоверные суждения никогда не могут быть следствиями правдоподобных суждений; б) законы логики имеют смысл, отличный от смысла законов психологии, поскольку первые относятся к истине и лжи, а вторые - к отношениям и связям между психическими явлениями; в) несмотря на то, что логика является дисциплиной, изучающей условия правильного мышления, а мышление - это психическая деятельность, из этого не следует, что логика - это часть психологии или основывается на ней; с арифметикой или алгеброй ситуация аналогична, ибо хотя вычисления представляют собой психическую деятельность, все же законы математики относятся к связям между числами и прочими математическими объектами; г) путаница логики с психологией происходит, главным образом, из-за терминологических неясностей, поскольку в обоих дисциплинах используются одни и те же выражения, например, суждение, которое в психологии означает убеждение, а в логике - объективный коррелят психического акта.

Аргументы а) и б) Лукасевич заимствовал у Гуссерля.[1] Обсуждаемая здесь работа носит выразительные следы влияния творца феноменологии и поэтому небезынтересным может оказаться более позднее мнение Лукасевича. Он пишет: “Первый том логических исследований Гуссерля произвел во Львове огромное впечатление, особенно на меня. Уже давно я не любил психологизм, разрабатываемый Твардовским, сейчас я порвал с ним окончательно. Однако второй том логических исследований Гуссерля меня разочаровал. В нем опять содержалась какая-то туманная философская говорильня, которая отталкивала меня от всех немецких философов. Я удивлялся, что такое различие может возникнуть между двумя томами одного и того же произведения. Позже я убедился, что в первом томе логических исследований ко мне обращался не Гуссерль, только некто значительно больший, чем он, тот, кого Гуссерль использовал в своей книге, а был им Готтлоб Фреге”.[2]

После появления статьи Лукасевича ситуация очень быстро изменилась. Работа Лукасевича была принята доброжелательно в среде молодых философов, которым, начиная с 1906 г., он читал лекции по логике. К вопросу о психологизме Лукасевич вернулся в учебнике “Элементы математической логики”(1929), в котором атаковал т.н. философскую логику как конгломерат различных вопросов - эпистемологических, логических и психологических, приводящих к смешению предметов исследований отдельных наук. Много позже [1951а] Лукасевич подтвердил свое мнение о психологизме: “ То, что называется “психологизмом” в логике, -признак упадка логики в современной философии” (С. 48)

Представленный выше аналитический метод Лукасевич считал средством достижения целей в философии, в частности, в метафизике. К области исследования последней он относил наряду с "теорией целостности", "теорией последовательностей" также и "общую теорию необходимых отношений". Изучением "необходимых отношений - считает Лукасевич - до сих пор никто не пробовал систематически заниматься. Современная философия попросту не понимала исследований этого вида. Из различных необходимых отношений занимались главным образом отношениями причинности; но и исследование в области причинности она проводила присущим ей психологическим способом".[1907, S.55]

Итак, понятие причины - это лишь один предмет из множества абстрактных реальных предметов, которым присущи общие черты, т.е. имеет место аналогия между такими предметами. Она устанавливается прежде всего на основании существования предмета, возможно, косвенным образом, когда существование одного предмета подтверждает существование другого, как, например, понятие причинности и суждение. Так Лукасевич считает, что "каждый член отношения причинности удается выразить в экзистенциальной форме и это следует из определенного значения понятия "существовать". Это слово - пишет Лукасевич - мы очень часто употребляем в значении "быть истинным" [byc naprawde], а следовательно, быть предметом истинного [prawdziwego] утвердительного суждения. Поэтому в сущности, если два отношения принадлежности некоего свойства данному реальному предмету связаны узлом причинности, то в таком случае истинность, соответственно ложность, суждений, относящихся к этим отношениям принадлежности связаны отношением основания и следствия". [1907, S.50] Другой важной характеристикой отношения причинности является, по мнению Лукасевича, отсутствие "специального временного отношения, которое бы нас принуждало к определению причины как предмета одновременно со следствием, либо упреждало его". Вот эти главнейшие свойства отношения причинности, составляющие аналогию с логическим отношением основания и следствия, позволяют Лукасевичу использовать дедуктивный метод как в области суждений, так и в области абстрактных предметов, хотя часто и неявно, а иногда - очевидным образом, например, для истинностных значений. В дальнейшем эта аналогия, предваряемая анализом, приведет Лукасевича к созданию многозначных логик, разложивших, казалось бы нерасчленимое - абстрактный предмет "истину", ибо отношения, ставшие центральным пунктом его анализа, в частности, интралингвистические отношения, потребуют интерпретации не только в языке, но и в действительности. Позже отмеченная аналогия несколько ослабнет и взгляды Лукасевича изменяться, например, на отношение причинности [1922], но в целом его подход к научным исследованиям останется прежним, вершиной которого будет дедуктивный метод. Метод же индуктивный, который составляет ядро аналитической философии, рассматривавшей наряду с явлениями действительности и их выражения в языке, являющиеся также предметами этого метода, будет Лукасевичем оставлен окончательно, что и знаменует второй период его творчества, логический. В выступлении на II Польском философском съезде в 1927 году программа построения научной философии в глазах Лукасевича выглядела следующим образом: "Будущая философия должна начать свое строительство с самого начала, с фундаментов. Начать же с фундаментов - это значит сначала пересмотреть вопросы, которые можно сформулировать понятно, отбросив все прочие. Уже в этой предварительной работе математическая логика может быть полезна, т.к. она установит значение многих выражений, относящихся к философии. Затем следует приступить к решению тех вопросов, которые можно сформулировать понятно. Наиболее соответствующим методом, который следовало бы с этой целью применить, кажется, опять же должен быть метод математической логики, дедуктивный метод, аксиоматический. Основываться следует на предложениях по возможности интуитивно ясных и определенных и такие предложения следует принять как аксиомы. Первичными, т.е. неопределяемыми понятиями нужно выбрать такие выражения, смысл которых можно всесторонне выяснить на примерах, нужно стараться, чтобы аксиом и первичных понятий было как можно меньше и нужно их все точно учитывать. Все прочие понятия должны быть безусловно определяемы на основе первичных понятий, а все прочие утверждения - безусловно доказуемы на основании аксиом и при помощи принятых в логике методов доказательства. Полученные таким образом следствия необходимо непрестанно контролировать данными интуиции и опыта, а также результатами прочих наук, особенно естественных. В случае необходимости следует систему подправлять, формулируя новые аксиомы и подбирая новые первичные понятия. О контакте с действительностью следует заботиться постоянно с тем, чтобы не образовывать мифологического бытия типа платоновских идей или вещей-в-себе Канта, но познать сущность и строение того реального мира, в котором мы живем и вершим, и который хотим как-то преобразовать в [мир] лучший и совершеннейший. В этой работе покамест нужно себя вести так, как будто в философии до сих пор ничего не сделано".[1928, S.4]

Важнейший вывод, который можно сделать из приведенной программы реформ Лукасевича - это усечение философии в методе и предписывание ей пользоваться только результатами, отметая большинство процессов, прежде всего психологических, оставляя единственно в употреблении процессы дедукции. Тем самым сужая использование метода, Лукасевич сужает философию и в предмете, полагая таковым, в качестве примера и представителя, мейнонговский объектив как коррелят такого предмета. ([1907], s.64) Сложность программы Лукасевича заключалась не в том, что он не сумел найти метафизическим предметам, в качестве которых он видел прежде всего отношения действительности, логические отношения, но в том, что для обратной операции, называемой интерпретацией им даже не делались попытки отыскания экстралингвистических предметов. Единственным таким предметом как коррелятом для Лукасевича было истинностное значение, а поэтому апелляция к объективу Мейнонга носила сугубо иллюстративный характер, поэтому специализацией польской логики, одним из создателей которой был Лукасевич, стала логика предложений, а не предикатов.

Анализ следующей малоизвестной работы о Декарте [1938] демонстрирует установку польского ученого на формальнологический метод, который независим от онтологических предпосылок. В статье разбирается фундаментальный декартовский тезис: cogito, ergo sum. Высказывание, выражающее приведенный принцип, Лукасевич трактует не как предложение, но как сокращение вывода. В этом случае возникает не вопрос истинности высказывания "думаю, следовательно существую", а вопрос правильности рассуждения, для которого это выражение выступает сокращением. Это сокращение, считает Лукасевич, является просто энтимематической записью рассуждения о посылках "если думаю, то существую", "думаю" и заключении - "существую". Вопрос истинности декартовского высказывания таким образом зависит от посылок. Возникает возможность признать высказывание "если думаю, то существую" особым случаем некоторого общего закона, провозглашающего, что если некоторый предмет является каким-то предметом, в частности что-то делающим, то он существует. По мнению Лукасевича такой закон можно доказать на основании одной из теорий Лесьневского - Онтологии, тогда как вторая посылка декартовского рассуждения - "думаю", может быть понята как эмпирическое предложение, почерпнутое из психологического опыта. Лукасевич не высказывается о законности декартовского тезиса, но только предлагает его следующее обоснование: если мы хотим с использованием современного состояния знаний принять аксиому Декарта, то следует это делать указанным выше способом. А способ этот дополняет изложенный выше абрис программы реформ философии.

Итак, если ранее Лукасевич считал, что логика может предоставить философии определенный методологический образец (аксиоматический метод), то позже в [1938] он высказывает допущение, что логика может предоставить философии предпосылки по существу, в данном случае, онтологические. Очевидно, что при такой интерпретации логика начинает играть роль общей теории предметов.

Лукасевич высказывал и третий способ применения логики в философии: "Сегодня мы знаем, что существуют не только различные системы геометрии, но и различные системы логики, которые к тому же обладают тем свойством, что одни из них нельзя перевести в другие. Я верю, что одна и только одна из этих логических систем реализована в действительном мире, т.е. является реальной так, как одна и только одна геометрическая система реальна. Правда, сегодня мы не знаем, какая это система, но не сомневаюсь, что эмпирические исследования когда-нибудь покажут [...], соответствует ли эта связь одних фактов с другими двузначной логике, или же какой-то многозначной. Все априорные системы в том момент, когда мы их применяем к действительности, становятся естественнонаучными гипотезами, которые следует проверять фактами так же, как и физические гипотезы. С этим взглядом связан также мой подход к вопросам метафизики." ([1936], S206/207) Из этой цитаты можно заключить, что утверждения логики могут выполнять роль посылок в философской аргументации, если будут трактоваться эмпирически, тогда как сама по себе логика не навязывает никаких онтологических решений. В статье “В защиту логистики” Лукасевич уточняет отношение логики и онтологии: "Я хорошо знаю, что все создаваемые логические системы при тех предположениях, при которых мы их создаем, необходимо истинны. Речь может идти только о проверке онтологических предположений, находящихся где-то на дне логики, и я думаю, что поступаю согласно с методами естественных наук, если хочу следствия этих предположений проверить фактами." ([1937], S.218) Таким образом, проверке не подлежат законы логических систем (интерпретированных или нет), но онтологические предпосылки, находящиеся в глубинной структуре логики и, возможно, такой структурой для Лукасевича был принцип двузначности.

В своем отношении к философии взгляды Лукасевича не претерпели каких-либо изменений и на всем протяжении творческого пути были стабильными: научная философия возможна и отдельные ее проблемы, главным образом онтологические, являются предметами философии как науки, а как наука она может и должна использовать индукцию и дедукцию. Однако в отношениях логики к философии взгляды Лукасевича можно понимать по-разному: от признания философской нейтральности утверждений логики через возможность онтологической их интерпретации (онтологических утверждений или глубинных предпосылок) до логики как обобщенной онтологии. Несомненной остается роль логики как универсального образца методологии для философии, а поэтому логика имеет громадное значение для последней. Столь же стабильным было отношением Лукасевича и к философии как совокупности воззрений на жизнь и мир, которые не соответствуют требованиям научной строгости, а поэтому, по крайней мере, в ближайшем будущем должны быть выведены за пределы науки.

Итак, для Лукасевича исходной позицией вступления во владения логики была метафизика. Оправдание метафизики он видел в необходимости отношений действительности, коррелятом которых считал отношения суждений. Необходимость этих последних обосновывается теорией дедукции. Именно в ней Лукасевич видел научный метод, который стал для него и объектом, причем метафизическим. Онтологический статус такого объекта так никогда и не был объяснен Лукасевичем, а его занятия модальной логикой, как кажется, являются неявным стремлением интерпретировать эти метафизические объекты.

§ 2. Влияние Я. Лукасевича на развитие математической логики во Львовско-Варшавской школе.

Несмотря на то, что систематическое изложение логики в Польше впервые состоялось в лекциях К.Твардовского, повторявшихся периодически каждые 4 года, оно происходило в философском обрамлении и роль математики специально не оговаривалась. Восприятию алгебры логики Буля или Шредера мешала интенциональная составляющая теории суждений Твардовского, погружающая все изложение в философский контекст, а точнее - онтологический; в такой манере преподавания логики объектом изучения оставался имманентный предмет в экстралингвистической сфере, а не сам метод рассуждения, являющийся объектом теории дедукции.

Первым учеником Твардовского, заинтересовавшимся логикой профессионально, был Лукасевич. С 1907 г. он начал читать во Львове лекции по логике. Важным событием в развитии логики в Польше оказалась монография Лукасевича о принципе противоречия у Аристотеля (1910). Польский исследователь Львовско-варшавской школы Я.Воленский [1985] выделяет троякую роль этой книжки. Во-первых, она содержала глубокий анализ оригинальных текстов Аристотеля, что было как бы предзнаменованием дальнейших революционных работ Лукасевича по истории логики; во-вторых, в ней приводились аргументы, указующие на необходимость доказательства принципа противоречия и это был определенный шаг в направлении многозначных логик; в-третьих, книжка Лукасевича была снабжена дополнением, содержащим изложение алгебры логики, а тем самым монография явилась в сущности первым учебником математической логики в Польше. О своих впечатлениях от прочтения этой книжки Лесьневский вспоминал: " В 1911 г. мне попала в руки книжка г.Лукасевича о принципе противоречия у Аристотеля. Из этой книжки, которая в свое время оказала значительное влияние на интеллектуальное развитие ряда польских "философов" и "философствующих" ученых моего поколения, а лично для меня оказалась откровением с разных точек зрения, я впервые узнал о существовании на свете "символической логики" г.Бертрана Рассела и его "антиномии", относящейся к "классу классов, не являющихся собственными элементами". ([1927], S.169) Появление книги послужило росту заинтересованности молодых польских философов математической логикой. Число логиков в окружении Твардовского и Лукасевича начало быстро увеличиваться и в нем оказались Айдукевич, Чежовский, Котарбинский, Качоровский, Лесьневский, Смолька и Завирский. На страницах "Пшегленда филозофичного" и "Руха филозофичного" упомянутые философы выступили с многочисленными работами и открыли дискуссии по вопросам, носящим логическую направленность. Айдукевич [1913] и Лукасевич [1913] писали об отношении следования, Лукасевич [1913a] - об основах исчисления правдоподобия, Завирский - о модальных предложениях, Смолька [1913], Чежовский [1913],[1918] и Лесьневский [1914],[1916] - о логических парадоксах. Отзвуки монографии Лукасевича [1910] можно найти в дискуссиях Котарбинского [1913a] и Лесьневского[1911],[1912],[1913],[1913a] по вопросам существования, будущих событий, истинности, принципа исключенного третьего и принципа противоречия. Заметное влияние на развитие логики и методологии в Польше имели работы Лукасевича об индукции [1903],[1906a],[1909], а особенно его статья "О творчестве в науке"[1912], содержащая популярную в Польше классификацию рассуждений, которая в несколько усовершенствованном виде с названием "О науке" была помещена в самоучителе [1915] и неоднократно переиздавалась.[3] Всем этим начинаниям "очистила" дорогу статья "Логика и психология" [1907], ясная и отчетливая критика психологизма которой была положительно воспринята в школе. Эта критика в значительной мере способствовала развитию математической логики в Польше, поскольку психологизм, популярный на рубеже XIX и XX веков, представлял собой барьер развитию математической логики.

Новый импульс распространению математической логики придал переезд Лукасевича в Варшаву, где он занял кафедру на естественно-математическом отделении университета; позже к нему присоединился Лесьневский, возглавивший кафедру философии математики.[4] Появление обоих логиков с философской родословной в среде математиков оказало на последних заметное влияние и было воспринято доброжелательно. Пути же самих логиков заметно отличались: если Лукасевич пришел к математической логике в контексте успеха своих лекций среди математиков, то обращение Лесьневского произошло в одиночестве, путем индивидуальных размышлений; если Лукасевич в своей работе не выходил за пределы признанной в то время парадигмы логики, то Лесьневский стремился создать собственную парадигму. Небезынтересно следующее сравнение обоих логиков, данное их учеником и сотрудником Собоцинским ([1957], S.42/43): "Между Лукасевичем и Лесьневским, двумя великими фигурами варшавской логической школы [...] имеется существенная разница. Лесьневский был также философом по образованию, и также отстранился от философии [...]. Однако в противовес Лукасевичу он считал, что можно найти "настоящую" систему логики и математики. Его систематизация основ математики не была исключительно постулативной; он стремился дать в дедуктивной форме наиболее общие законы построения действительности. По этой причине он мало использовал математические и логические теории, которые - даже тогда, когда они были непротиворечивы - он не считал подходящими для фундаментальных, структурных законов действительности. По этой же причине он концентрировал свои исследования на определенной системе, которую сам и построил, и на ее внутренних проблемах, ибо был уверен, что эта система единственная и настоящая. Таким образом, хотя в определенном смысле Лесьневский никогда не обращался к философии, он может быть признан философом логики, одним из величайших в этой малой группе [...]. У Лукасевича таких забот не было. Он не пробовал строить окончательную систему оснований дедуктивных наук. Его целью было [...] предоставление многим областям нашего мышления точных и элегантных структур [...]. Он интересовался прежде всего проблемами дедукции, ее совершенства и аксиоматизации [...], считая, что стоит исследовать каждую область, в которой может быть использована (значимо, или нет) дедукция".[5]

 Первое изложение исчисления предложений в Польше также принадлежит Лукасевичу. В работе "Двузначная логика" [1920b] излагаемое исчисление представлено как нечто отличное от алгебры логики и совершенно отчетливо связано с уже устоявшейся парадигмой математической логики. Рассматриваемая Лукасевичем система сформулирована в языке, содержащем пропозициональные переменные (p,q,r,...), константы 0 (ложь) и 1 (истина), логические связки: ® (импликация), ù (отрицание), а также знаки : П (универсальный квантор), U (утверждение) и N (отбрасывание). Аксиомы имеют следующий вид:

U: Пp( 0 ® p);

U: Пp( p ® 1);

N: 1 ® 0.

Лукасевич вводит четыре дефиниции:

дефиниция отрицания - U: Пp(ù p=p ® 0);

дефиниция дизъюнкции - U: Пpq (pÚ q = (p ® q) ® q);

дефиниция конъюнкции - U: Пpq ((pÙ q) = ù (ù pÚù q));

дефиниция эквивалентности - U: Пpq(p « q = (p ® q) Ù (q ® p)).

Утверждения получаются из аксиом и дефиниций при помощи следующих правил вывода:

1. Каждое выражение принадлежит исчислению, если оно возникает из утверждения, содержащего переменные и квантор, посредством подстановки 0 или 1 на место переменных.

2. Каждое выражение, эквивалентное некоторому выражению, принадлежащему системе, также принадлежит исчислению; каждое выражение можно отбросить, если оно эквивалентно отбрасываемому выражению.

3. Каждое выражение принадлежит исчислению, если оно в результате подстановки 1 вместо выражения исчисления, или 0 вместо выражения, не принадлежащего исчислению, переходит в утверждение; можно отбросить каждое выражение, которое в результате такой подстановки переходит в отбрасываемое выражение.

4. Каждое выражение, содержащее переменные и кванторы , в которое вместо переменных подставляются 1 и 0, принадлежит исчислению, если в результате такой подстановки получаются исключительно утверждения системы.

Эти правила вывода Лукасевич считал очевидными, исходя из свойств введенных символов, и полагал их обоснование достаточным. Свойства логических функторов эксплицировались при помощи записей, эквивалентных истинностнозначным таблицам; приводилась также табличная процедура проверки истинности утверждений. Затем Лукасевич из аксиом и дефиниций выводит 40 утверждений исчисления высказываний.

Табличный метод проверки истинности предложений не является результатом оригинальной идеи Лукасевича и был известен ранее, но в его работе едва ли не впервые этот способ проверки истинности обсужден систематически. Необходимо отметить трактовку истинностных значений в духе Фреге как денотатов предложений и введение наряду с правилами утверждения также правил отбрасывания, которые позже будут использованы при формализации логики Аристотеля и модальной логики. Дефиниция дизъюнкции сформулирована таким образом, что может быть использована и в трехзначной логике. Таким образом, в обсуждаемой работе содержаться идеи, которые позже будут развиты в трудах варшавской школы логики.

И все же логическая система в статье [1920b] все еще весьма несовершенна. Прежде всего Лукасевич не различает теорию и метатеорию, поскольку функтор импликации воспроизводится им при помощи оборотов "если, то" и "следует", а этот последний принадлежит метаязыку; подобное же происходит и с символами утверждения и отбрасывания. Состав и формулирование правил вывода усложнены и это является следствием присутствия в посылках кванторов, которые Лукасевич ввел руководствуясь идеями Лесьневского, но они не играют в системе из [1920b] такой роли, как в Прототетике и приводят к излишним сложностям. В итоге эта система представляет собой смесь различных идей и намерений, некоторые из которых позже были развиты, а другие - отброшены.

Начиная с 1920 г. преподавание логики на естественно-математическом отделении Варшавского университета расширилось: были введены спецкурсы, семинары и прочие формы обучения. Заинтересованность студентов-математиков логикой постепенно возрастает и многие выбирают ее своей специализацией. В конце 20-х годов заканчивают учебу и приступают к научной работе в области логики Тарский, Вайсберг, Линденбаум, Ясковский, Пресбургер и Собоцинский (последний был философом по образованию), а в тридцатые годы к ним присоединяются Мостовский, Слупецкий и Леевский. Семинары Лесьневского и Лукасевича представляют собой научные коллективы, интенсивно работающие над проблемами логики. Все заметнее становится ведущая роль Тарского, который написав докторскую диссертацию под руководством Лесьневского затем перешел к сотрудничеству с Лукасевичем.[6] Влияние обоих корифеев школы, исповедывавших различные парадигмы философии языка (философии имени - Лесьневским  и философии предложения - Лукасевичем), сказалось со всей силой в эпохальном творении Тарского - формулировании критерия истинности.

Несомненно решающим фактором развития логики в Варшаве было нахождение Лесьневского и Лукасевича в среде математиков, которые, о чем уже упоминалось, приязненно встретили львовских отступников философии. В среде варшавских математиков сложился особенно благоприятный климат для развития логики и в этой среде Лукасевич и Лесьневский считались нормальными партнерами научной деятельности. Они не считали себя математиками, не хотели и уже не могли быть философами и в этой ситуации были обречены стать логиками. Логика трактовалась ими как наука, тесно связанная с математикой, но и автономная.[7]

Постулируя автономность логики, вызванную эмансипацией не только от математики, но в первую очередь от философии, Лукасевич и Лесьневский, невзирая на отступнические заверения, все же сохранили связь с философией в том смысле, что старались понять смысл утверждений логики и их интуитивную мотивацию; разрыв с философией касался единственно способа философских спекуляций.[8]

Другое объяснение феномена школы, дополняющее вышеприведенные соображения, хотя и носит психологический характер, все же, как кажется, имеет место. Психологические мотивы бывших львовских философов и варшавских математиков совпадали, что и создало тот климат, о котором сказано выше. А именно, возрождение независимой Польши в патриотически настроенных умах и душах вызвало порыв самоутверждения, подкрепляемый признанием "со стороны". С этой целью варшавскими математиками были сознательно выбраны те области этой дисциплины, в которых, если не завоевать признание было легче, то, по крайней мере, обратить на себя внимание; с этой целью были выбраны топология и теория множеств. Львовские математики во главе с Х.Штейнгаузом и Ст.Банахом таких забот не знали и до тесного сотрудничества между ними и философами дело не дошло, хотя попытка повторить варшавский эффект во Львове и была сделана в 1930 г., когда открылась кафедра математической логики, занятая Л.Хвистеком, а не Тарским, также претендовавшим на нее. Работая в новых областях математики варшавские ученые нуждались в поддержке, а таковую (не только психологически) предоставляла логика, контролируя каждый шаг на неизведанном пути. С другой стороны, для логиков, оставивших философские спекуляции, связанные не в последнюю очередь с вопросами существования, математика предоставила структуры, существование объектов в которых было самодостаточным. Коротко говоря, варшавские математики и логики нуждались друг в друге и сумели превратить психологические предпосылки в ту область человеческого знания, которая получила позже название метаматематики.

Продолжая науковедческие рефлексии о развитии варшавской логической школе трудно выделить Лукасевича как одинокого лидера, но в теории дедукции он был несомненно зачинателем и главным действующим лицом. Акцент на дедукции как главном методе научной деятельности, а также автономность логики, или лучше сказать, ее независимость от математики и философии привели к тому, что лозунг "логика для логики" стал общепринятым в школе. Этот лозунг выражает также и существенные свойства теории дедукции, например, замкнутость ее процессов относительно результатов, т.е. формул. В школе ставились многочисленные рекорды, например, предлагалось отыскать различные кратчайшие аксиоматики исчисления высказываний. Подобные "задачи" в сочетании с трехгодичным курсом логики для студентов-математиков привели к тому, что многие из них начинали специализироваться в логике. Атмосферу, царящую в варшавской среде логиков хорошо передает вступление к широко известной статье Лукасевича и Тарского "Исследования исчисления высказываний" : "В последние годы в Варшаве проводились исследования, относящиеся к той части метаматематики, или лучше - металогики, областью исследований которой является простейшая дедуктивная дисциплина, а именно, т.н. исчисление предложений. Эти исследования инициировал Лукасевич; первые результаты принадлежат также ему и Тарскому. На семинаре математической логики, проводимом с 1926 г. под руководством Лукасевича в Варшавском университете, получено и обсуждено большинство результатов Линденбаума, Собоцинского и Вайсберга. Систематизацию всех этих результатов и уточнение используемых в них понятий произвел Тарский".([1930], S.129) А в Предисловии к своим "Элементам математической логики" Лукасевич писал: "Пожалуй, наиболее я обязан той научной атмосфере, которая сложилась в области математической логики в Варшавском университете. В дискуссиях с моими коллегами, главным образом с г.проф.Ст.Лесьневским и г.доц.др. А.Тарским, а часто с моими и их учениками, я ни одно понятие выяснил для себя, присвоил ни один способ выражаться и ни об одном новом результате узнал, о которых сегодня уже не смог бы сказать кому принадлежит их авторство." ([1929], S.9)

И наконец, успехи в логике варшавской части этой философской школы объясняются во многом организационными факторами, которые "вызвал к жизни" опять же главным образом Лукасевич. Все же следует заметить, что не столько организационные формы, сколько позиция львовских учеников Твардовского, повторивших методологические установки своего учителя, способствовала возникновению таких форм. Это замечание относится прежде всего к Лукасевичу и Котарбинскому. Так уже во Львове существовала логическая секция Польского философского общества. Такая же секция существовала и в Варшавском философском институте, а позже - в Польском философском обществе в Варшаве. Перед войной было начато издание I тома "Collectanea Logica" - специализированного журнала, посвященного логике и являющегося органом Польского логического общества; весь тираж этого тома был уничтожен во время бомбардировки Варшавы. Эпизодически выходили работы варшавских логиков в издании, которое можно было бы назвать препринтным, носящее заголовок "Studia Logica" и редактируемое Лукасевичем. Несомненно, появление институциональных форм является заслугой Лукасевича, считавшего, что автономно понимаемая логика как научная дисциплина требует отдельных организаций и отдельных изданий.

§ 3. Я.Лукасевич и история логических исследований во Львовско-варшавской школе.

(классическая логика)

В истории развития логики, главным образом классического пропозиционального исчисления, имя Лукасевича занимает в школе центральное место. Созданная им бесскобочная нотация считается визитной карточкой польской логической мысли. Во Львовско-варшавской школе этот вид записи формул использовался повсеместно (исключение составляет Лесьневский, но и он писал функторы перед аргументами).[9]

Следующая таблица устанавливает соответствие между одной из нотаций, использующей скобки, и польской записью функторов[10]:

отрицание	ù p	Np
импликация	p®q	Cpq
конъюнкция	pÙ q	Kpq
альтернатива	pÚ q	Apq
дизъюнкция	p/q	Dpq
эквивалентность	p«q	Epq

Два простых примера позволят объяснить использование бесскобочной символики. Рассмотрим формулы p ® (p®ù q) и (p ® p)®ù q. В т.н. польской нотации эти формулы имеют следующий вид: CpCpNq и CCppNq. Правильно построенная формула должна начинаться с заглавной литеры, т.е. с функтора, который одновременно является главным функтором всей формулы; в обоих примерах такой функтор обозначается литерой С (первое вхождение). Аргументом главного функтора является либо пропозициональная переменная (первый пример), либо формула, составленная из констант и переменных (второй пример). Для бесскобочной нотации существуют сугубо структурные критерии, устанавливающие, является ли данная последовательность, состоящая из больших букв и малых литер правильно построенной формулой.[11]

Рассмотрим критерий правильности построения формулы в бесскобочной нотации на примере исчисления предложений эквивалентности из работы Лукасевича [1939], критерия, который является незначительной модификацией аналогичного критерия Яськовского для системы, содержащей только функторы импликации и отрицания. Выражение, составленное из литер E и малых литер правильно построено тогда и только тогда, когда выполняются следующие два условия:

(1) число литер E, входящих в выражение, должно быть на единицу меньше числа малых литер;

(2) в каждой части последовательности, начинающейся в произвольном месте выражения и продолжающейся до его конца, число литер E должно быть меньше числа малых литер.

Оба условия независимы, что легко может быть показано на примерах. Так, выражением EpEqr выполняются оба условия и оно правильно построено. Выражение EpqEr выполняет первое условие, однако не выполняет второго, ибо в части, начинающейся со второй литеры E число литер E не меньше числа малых букв. Выражение pEEqrs выполняет второе условие, но не выполняет первое, т.к. число литер E в этом выражении не на одну, а на две литеры меньше числа малых букв. Наконец, выражение pqEErs не выполняет ни первого, ни второго условия. Последние три выражения не являются правильно построенными.

На основании приведенных условий Лукасевич формулирует правило, позволяющее установить правильность какого-либо выражения, составленного из малых и больших литер.

Правило проверки правильности произвольного выражения состоит в том, что вначале каждой литере E приписывается число -1, а каждой малой литере - +1. Затем последовательно, начиная с последнего правого числа, подчиненного литере, суммируем числа, продвигаясь налево, к началу выражения. Следующий пример поясняет эти действия:

 E E E p q E r s E t u

 1 2  3 4  3 2 3 2 1 2 1

Литере u соответствует +1, литере t - также +1; 1 плюс 1 дает 2. Литере E соответствует -1, а поэтому суммируя это значение с предыдущей суммой, т.е. 2+(-1)=1, результат подписываем под E. Если выражение правильно построено, то согласно первому условию сумма, соответствующая всему выражению и записанная в самом начале должна равняться 1, а согласно второму условию все частичные суммы, соответствующие отдельным отрезкам выражения, должны быть положительными. Достаточно взглянуть на приведенное в качестве примера выражение с тем, чтобы убедиться в его правильности.

Польская нотация является однозначной в том смысле, что каждая конечная правильно построенная последовательность больших и малых литер имеет один и только один перевод в стандартную нотацию, использующую скобки. Прагматический аспект польской записи анализируется Воленским [1985], который считает, что главным достоинством бесскобочной символики является экономия алфавита, поскольку польская нотация не требует вспомогательных знаков (точек, скобок) и правил группирования таких знаков (их числа и формы). Если в скобочной записи структура, а значит и смысл формулы определяются использованием скобок, то в польской символике структура формулы зависит исключительно от позиции литер. Однако с дидактической точки зрения символика Лукасевича считается интуитивно трудно воспринимаемой и поэтому большинство учебников по логике написаны с использованием скобок. Отмечается, что если речь идет о коротких формулах, то оба типа нотации имеют одинаковые возможности ориентации в структуре выражения, тогда как в формулах средней длины скобочная символика удобнее, но длинные формулы - считает польский исследователь школы - в бесскобочной записи более читабельны.[12].

Бесскобочная символика отражает определенные представления варшавских логиков, связанные со свойствами логических систем. Такие системы должны, конечно, удовлетворять основному условию - быть непротиворечивыми, но кроме этого, если возможно, быть полными и основываться на независимых аксиомах и первичных понятиях. Последнему условию, принимаемому обычно как желательное, а не обязательное в школе уделялось особое внимание и считалось, что взаимная зависимость первичных понятий и аксиом является серьезным недостатком.

В 20-е годы уже было известно, что исчисление высказываний можно построить, основываясь на различных системах первичных понятий и аксиом. Возник вопрос: можно ли и как сравнивать такие аксиоматики в предположении, что построенные на них исчисления высказываний являются непротиворечивыми и полными? Определенные критерии сравнения аксиоматик использовались давно. Так независимая система аксиом лучше зависимой. Далее, можно сказать, что лучшей является независимая аксиоматика, основывающаяся на независимых первичных понятиях, чем независимая аксиоматика, но основывающаяся на зависимых понятиях. Отсюда можно сделать вывод, что лучшей является аксиоматика, использующая меньшее число первичных терминов (понятий)[13].

В школе были сформулированы также дополнительные критерии. Они касались числа аксиом, их длины, числа различных переменных и т.н. органичности аксиом. Первый критерий прост: чем меньше аксиом содержит исчисление - тем оно лучше, поэтому оптимальной является одноэлементная аксиоматика. Этой позиции, как было показано ранее, придерживался Лесьневский. Определим длину аксиоматики числом входящих в нее символов. Из двух аксиоматик, содержащих одинаковое число первичных символов и одинаковое число аксиом, лучшей является более короткая аксиоматика. Предположим, что существуют две аксиоматики одной длины, но записанные при помощи различных переменных. В этом случае лучшей является аксиоматика, содержащая меньше отличных друг от друга переменных. Органичной называется такая формула системы, никакая собственная часть которой не принадлежит исчислению; например, формула CqCpp является неорганичной. Из двух аксиом - органичной и неорганичной лучшей является аксиома органичная. Понятие органичной формулы происходит от Лесьневского, а ее дефиниция - от Вайсберга. Впервые она была опубликована Лукасевичем и Тарским[1930a]. В конечном счете идеальная аксиоматика должна состоять из одной органичной аксиомы минимальной длины и по возможности с наименьшим числом различных символов. Наиболее естественно приведенные критерии применимы к исчислениям высказываний, но в школе искали подобные критерии и для более богатых систем. Так Линденбаум [1936] привел критерий простоты для произвольных функторов, заключающийся в том, что функтор F₁ проще функтора F₂, если число аргументов F₁ меньше числа аргументов функтора F₂, а в случае, если оба функтора имеют одинаковое число аргументов, то F₁ будет проще, если по крайней мере один из его аргументов будет более низкого логического типа, чем произвольный аргумент F₂ и никакой аргумент F₁ не принадлежит к более высокому типу, нежели произвольный аргумент F₂. Этот критерий применим, например, к системам Лесьневского.

Приведенные критерии отражают культивируемый в варшавской части школы лозунг «логика для логики». Ниже приводится обзор некоторых результатов классического исчисления высказываний.

Наиболее известной системой исчисления высказываний является система, основанная на импликации и отрицании как первичных терминах. В школе был известен ряд аксиоматик этой системы. Одна из первых принадлежит Лукасевичу [1925], а все исчисление подробно изложено в [1929]. В качестве аксиом Лукасевич принимает следующие формулы:

(1) CCpqCCqrCpr

(2) CCNppp

(3) CpCNpq

Правилами вывода являются правила подстановки, отделения и замены по определению. Последнее правило сформулировано следующим образом: если x доказуемо в исчислении, а y есть часть x, эквиморфная правой стороне одной из дефиниций Dpq=CNpq, Kpq=NCpNq, Apq=CpNq, Epq=NCCpqNCqp относительно подстановки, то каждое выражение, полученное из x заменой y выражением эквиморфным с левой стороной дефиниции либо ее подстановкой, является доказуемым в системе.

Таким образом, в основе исчисления лежат правила подстановки, отделения и замены по определению. В варшавской школе схемы аксиом использовались только при формализации металогических и метаматематических исследований; конструкции же логических систем были сформулированы исключительно при помощи конкретных формул. Символ равенства по определению (“=”) не принадлежит языку системы. Лукасевич трактует дефиниции как сокращения, считая их теоретически излишними. Лесьневский же в вопросе о дефинициях занимал иную позицию, но и Лукасевич позже изменил взгляд на дефиниции, о чем будет сказано ниже. Так в рассматриваемой системе роль дефиниций сугубо прагматическая, ибо они не носят характер творческий и Лукасевич считает, что дефиниции не являются доказуемыми выражениями, но лишь "равенствами на полях теории".

Из аксиом (1)-(3) при помощи правил подстановки, отделения и замены Лукасевич выводит 143 формулы исчисления высказываний. Доказательство занимает 19 страниц и с учетом словесного комментария для столь значительной части пропозиционального исчисления должно считаться весьма компактным,. Этот эффект был достигнут благодаря использованию экономичного метода записи структуры доказательства. Пример поясняет метод Лукасевича[14]:

             (1)p/Cpq,  q/CCqrCpr,  r/s  *C(1)-(4)

(4)          CCCCqrCprsCCpqs.

Реконструкция доказательства формулы (4) состоит из следующих шагов. В аксиому (1) производится подстановка: вместо переменной p - выражение Cpq (этому шагу соответствует секвенция (1)p/Cpq), вместо переменной q - выражение CCqrCpr (секвенция q/CCqrCpr), вместо переменной r - переменная s (секвенция r/s); все подстановки совершаются в аксиому (1), что в строке доказательства сигнализируется тем, что между первым вхождением литеры p в этой строке и последним вхождением s (последняя литера перед звездочкой) не находится ни один номер аксиомы или формулы. После подстановки получается выражение CCCpqCCqrCprCCCCqrCprsCCpqs. Посылка этой импликации (главного функтора С), т.е. выражение, начинающееся вторым вхождением литеры С и кончающееся вторым вхождением r, представляет собой аксиому (1), а следствие - доказуемую формулу. Поскольку подстановка осуществлялась в формулу исчисления, а настоящая формула является таковой, и правило подстановки говорит, что результат подстановки также принадлежит исчислению, то можно применить правило отделения, о чем информирует последовательность *C(1)-(4).

Описанный способ доказательства в дальнейшем использовался учениками Лукасевича.[15]

Помимо исчисления, основанного на аксиомах (1)-(3) в варшавской школе использовались и другие импликативные аксиоматики. Вот некоторые трехэлементные системы аксиом: CCCpqrCNpr, CCCpqrCqr, CCNprCCqrCCpqr - Лукасевич [1929]; CpCqp, CCpCqrCCpqCpr, CCNprCCqrCCpqr - Лукасевич [1930]; CNpCpq, CpCqCrp, CCNprCCqrCCpqr - Собоцинский [1954]; CCpqCNqCpr, CpCqCrp, CCNpqCCpqq - Собоцинский [1954].

Все приведенные импликативно-негативные аксиоматики используют те же правила и дефиниции, что и логическая система, представленная аксиомами (1)-(3).

В 20-е годы Лукасевич поставил задачу нахождения одноэлементного импликативно-негативного базиса (базис = аксиоматика). История поисков (изложенная в Собоцинский [1932] и частично в Лукасевич [1936], а более полно в Воленский [1985]) такова:

Тарский (1925) - аксиома из 53 литер:

СССССsCtCtCvCvvCCCCCpCqrCCpqCprCCCNpNqCqpxxyyCCpCqpzz;

Лукасевич (1927) - аксиома из 43 литер:

CCCsCtCtCpCqpCCCCCpCqrCCpqCprCCCNpNqCqpvvee;

Лукасевич (1927) - аксиома из 39 литер:

СССaCbCdaCCCCCpCqrCCpqCprCCCNpNqCqpvvee;

Лукасевич (1927) - аксиома из 38 литер:

СССaCbCdCedCCCNstCCNsNtsCCCpqCCqrCprzz;

Собоцинский (1927) - аксиома из 36 литер:

CCCaCbCdaCCCNmCqCNrNpCCmCqrCCpqCpree;

Лукасевич (1927) - аксиома из 35 литер:

CCCaCbCdaCCCNmCqCqNpCCmCqrCCpqCpree;

Лукасевич (1927) - аксиома из 33 литер:

CCCpCqpCCCNrCsNtCCrCsuCCtsCtuvCwv;

Этот далеко не полный список заключает аксиома Лукасевича, состоящая из 23 литер:

CCCpqCCCNrNstrCuCCrpCsp.

Поиск кратчайшей импликативно-негативной аксиомы не сводился исключительно к вопросу о числе литер. Варшавские логики искали также и органическую аксиому. Таковой является 27 буквенная аксиома Собоцинского (1927): CCCpqCCCNpNrsCrtCuCCtpCvCrp.

В школе исследовались также аксиоматики, использующие другие первичные термины. Лукасевич [1930] приводит дизъюнктивно-негативную аксиоматику: ANANANpqrANpr, ANANApqrANpr, ANANApqrANqr с правилами подстановки, отделения (если ANxy и x суть истинные формулы, то y - также истинная формула), дефинициями оставшихся функторов и правилами замены по определению. Особенно важна дефиниция Cpq=ANpq, которая позволяет представить аксиомы в следующем виде: CCApqrCpr, CCApqrCqr, CCprCCqrCApqr; эти аксиомы являются дизъюнктивно-импликативными и в явном виде отрицания не содержат.

Вайсберг [1938] сформулировал аксиоматику, в которой первичными терминами являются C и 0 (ложь): CpCqp, CCpqCCqrCpr, CCCpqpp, C0p + правило подстановки, правило отделения, дефиниции, например, Np=Cp0, а также правило замены по определению. Правило замены по определению привлекло внимание польских логиков в связи с функцией Шеффера, обнаружившего две взаимно дуальные двухаргументные функции, позволяющие определять все функторы классической логики.[16] В использовании функций Шеффера для аксиоматизации классического исчисления высказываний первым успехов добился Нико (Nicod) [1917]. Его аксиоматика содержала единственную аксиому DDpDqrDDtDttDDsqDDpsDps, правило подстановки и правило отделения (если DxDxy и x суть истинные формулы, то и y также истинная формула). Лукасевич [1931], заменяя в аксиоме Нико переменную t переменной s, получил формулу DDpDqrDDsDssDDsqDDpsDps. Она является частным случаем исходной формулы и вместе с тем аксиома Нико следует из аксиомы Лукасевича. Этот факт Лукасевич считал контрпримером известному мнению будто дедукция не обобщает и ставил вопрос: "Могут ли и какие общие черты иметь обобщающие формулы?" ([1931], S,174) Однако обе аксиомы являются неорганичными (в аксиоме Нико это выражение DtDtt, а у Лукасевича - DsDss). Позже Лукасевичем [1931] и Вайсбергом были найдены органические аксиомы исчисления предложений, использующие исключительно функтор строгой дизъюнкции. Во всех дизъюнктивных системах, кроме уже упомянутых правил подстановки и отделения, принималось также правило замены, предполагающее дефиницию функторов N, K, A, C, E при помощи функтора D.

Логики варшавской школы строили также аксиоматики с использованием большего числа первичных терминов. В работе Вайсберга [1937] приведена, например, следующая аксиоматика: CpCqp, CCpCqrCCpqCpr, CKpqp, CKpqq, CCpqCCprCpKqr, CpApq, CqAqp, CCprCCqrCApqr, CEpqCpq, CEpqCqp, CCpqCCqpEpq, CNpCpq, CCpNpNp с правилами подстановки и отделения. Тарский [1938] приводит схемы аксиом (в связи с чем ему достаточно правила отделения) с метапеременными следующего вида: CxCyx, CCxCyzCCxzCyz, CxAxy, CyAxy, CCxzCCyzCAxyz, CKxyx, CKxyy, CCzxCCzyCzKxy, CCNxxx, CCxNxNx.

В школе исследовались также и частичные исчисления высказываний. Частичным называется исчисление, основанное только на некоторых функторах, которых недостаточно для определения всех постоянных первичных терминов исчисления. Так в 1921 г. Тарский опубликовал аксиоматику для импликативного исчисления высказываний: CpCqp, CCpqCCqrCpr, CCCpqrCCprr с правилами подстановки и отделения (Лукасевич, Тарский [1930]). Ряд аксиоматик этого вида принадлежит Вайсбергу.

Изучалась возможность построения импликативного исчисления на одной аксиоме.[17] Вайсберг (1926) обнародовал 25-и буквенную аксиому (органическую): CCCpqCCrstCCuCCrstCCpuCst, а Лукасевич (1926) привел также 25-и буквенную аксиому, но не органическую: CCCpCqpCCCCCrstuCCsuCruvv. Дальнейшие результаты получил Лукасевич, который сформулировал (1930) органичную 17-и буквенную аксиому CCCpqCrsCtCCspCrp, а затем (1936) - 13-и буквенную, также органичную аксиому: CCCpqrCCrpCsp. Вопрос был окончательно решен, когда Лукасевич [1948] опубликовал доказательство того, что аксиома из 13-и литер является кратчайшей.

Первую аксиоматику, использующую эквивалентность в качестве единственного постоянного термина, привел Лесьневский [1929]: EEEprEqpErq, EEpEqrEEpqr + правила подстановки и отделения. После появления ряда аксиоматик, полученных Вайсбергом, Бриманом, Лукасевичем и Собоцинским Лукасевич [1938] доказывает, что формула, содержащая менее 10 литер не может быть единственной аксиомой исчисления, построенного исключительно на функторе эквивалентности.

§ 4. Пропозициональное исчисление с переменными функторами.

Весьма интересным и редко обсуждаемом случаем логической теории является исчисление предложений с переменными функторами. Его появление в определенной степени связано с точкой зрения Лукасевича на определения. Выше упоминалось, что Лукасевич понимал дефиниции как метаязыковые сокращения. Отличную от этой позицию в школе занимал Лесьневский, который трактовал дефиниции как предложения системы. Сравнение этих двух точек зрения побудило Лукасевича к изучению исчисления предложений с переменными функторами, введенными впервые в Прототетике Лесьневского. Первый раз этим вопросом Лукасевич занялся в статье об исчислении предложений эквивалентности [1939]. Лукасевич замечает, что выражение Vp (verum от p) как одноаргументный функтор от пропозициональной переменной может быть введен двояко:

 D₁        Vp =df Epp

 D₂        EVpEpp

Отличия D₁ и D₂ состоят в том, что D₁ записано в метаязыке, а D₂ является предложением исчисления, но кроме того эти определения "методологически разные" и, как замечает Лукасевич, не находя лучшего выражения, D₂ "действует "творчески"". Различия определений D₁ и D₂ демонстрируются на примере выражения

(I)      EEsEppEEsEppEEpqEErqEpr,                                                                                                  

которое является выводимой формулой исчисления эквивалентностей. Особенность этой формулы состоит в том, что все ее заключения можно получить исключительно путем подстановки, но не отделением. Тот факт, что формула (I) "неделима" Лукасевич показывает методом, восходящим к Тарскому.[18]

А именно, если из (I) мы хотим получить новую формулу путем отделения, то должны предположить, что существуют две подстановки в (I), одна из которых имеет тип Exy, а вторая - x (все переменные принадлежат метаязыку, т.е. являются переменными, значениями которых суть произвольные выражения языка исчисления эквивалентностей). Эти семиотические условия записываются следующим образом:

(a)      Exy :=: EEaEbbEEcEddEEdeEEfeEeg

(b)          x :=: EEhEiiEEhEiiEEijEEkjEik

(символ :=: означает здесь эквиморфность).

В (а) литере x соответствует выражение EaEbb, т.е.

(c)          x :=: EaEbb,

тогда как из (b) и (c) получаем, что

                          (d)        EaEbb :=: EEhEiiEEhEiiEEijEEkjEik.

Отсюда вытекает, что следующие выражения эквиморфны:

                          (е)       a :=: EhEii

                          (f)        b :=: EhEii

                          (g)       b :=: EEijEEkjEik.

Из (f) и (g) получаем:

                           (h)        h :=: Eij

                           (i)        i :=: Ekj

                           (j)        i :=: Eik.

Последнее выражение абсурдно, поскольку невозможно, чтобы "i" было эквиморфно некоторому выражению, содержащему "i" как свою собственную часть. Отсюда следует, что невозможно получить две подстановки формулы (I), которые были бы подстановками типа Exy и x. Таким образом, к выражению (I) не может быть применено правило отделения. Отсюда непосредственно следует, что из (I) нельзя вывести никакой более короткой формулы, в частности EEpqEErqEpr, которая была бы аксиомой исчисления высказываний.

Однако ситуация измениться, если принять D₂. Достаточно в (I) вместо переменной s подставить выражение Vp, чтобы после двукратного применения правила отделения получить аксиому EEpqEErqEpr. Следовательно, дефиниция D₂ креативна. Такое решение не удовлетворяет Лукасевича, поскольку D₂ вводит в систему выражение, не являющееся первичным, а потому и не характеризуемое аксиомами. Лукасевич [1939] заключает: "Ни в коем случае мы не должны придавать новые свойства первичным терминам системы. Первичные термины должны быть охарактеризованы исключительно аксиомами. Если мы занимаем такую позицию, то следовало бы по возможности избегать творческих определений" (S.249).

К этой проблематике Лукасевич вернулся в работе "О переменных функторах от пропозициональных аргументов"(1951). Рассматривая формулу Прототетики Лесьневского

(1)      CfpCfNpfq

он задается вопросом про область значений пропозициональной переменной, отмечая, что вместо переменной можно подставлять любое правильно построенное выражение, а также константы 0 и 1. Этот вопрос Лукасевич распространяет и на функторы, спрашивая: "Какова область значений функторной переменной f ?" Он полагает, что вместо переменной f в выражении fx, где x является каким-то правильно построенным предложением, можно подставить каждое значение, которое с выражением x образует правильно "построенное целое". Таковым может быть одноаргументный функтор N, или же выражение Cr, а также выражение CC00. Подставляя в (1) вместо f выражение Cr получим формулу CCrpCCrNpCrq, а подставляя выражение CC00 - формулу CCC00pCCC00NpCC00q. Однако этот тип подстановки не охватывает все возможные случаи, поскольку из (1) невозможно получить ни CpCNpq, ибо при помощи подстановки невозможно устранить функторы, ни CCprCCNprCqr, т.к. никакая подстановка вместо f в выражениях fp либо fq не может переставить конечные p либо q со своего места. Эту трудность Лесьневский устраняет при помощи дефиниции, полагая, что Grp означает то же, что Crp. Подставляя в (1) Gr вместо f получим CGrpCGrNpGrq, а затем при помощи дефиниции - CCprCCNprCqr.

Предложенный Лесьневским способ Лукасевич считает искусственным и трудным. По мнению Лукасевича, он нашел новый тип подстановки, в котором символ fx, где x является пропозициональным выражением, представляет все правильно построенные выражения исчисления высказываний, содержащие x. Например, fp представляет Crp так же, как и Cpr, т.е. попросту представляет все пропозициональные выражения, содержащие p, включая само p, а также fp. С учетом такого представления Лукасевич считает необходимым ввести новое правило подстановки. Смысл правила подстановки с апострофом он поясняет на примере. Допустим, мы хотим из (1) получить формулу CCprCCNprCqr. Необходимую подстановку обозначим через f/C’. Это значит, что в (1) вместо f следует подставить выражение, начинающееся с C, кончающееся переменной r, а вместо апострофа везде вставить аргумент функтора f. Тогда fp переходит в Cpr, CfNp - в CCNpr, fq - в Cqr, а (1) - в искомую формулу CCprCCNprCqr. Теперь предположим, что из (1) мы хотим получить CpCNpq. С этой целью используем подстановку, обозначаемую сокращением f/’ , которая означает, что вместо f следует вписать переменную p , т.е. попросту миновать f.

Подстановка с апострофом имеет важные последствия при использовании дефиниций в дедуктивных системах. Лукасевич считает, что концепция определений, как сокращений, так и эквивалентности имеет свои преимущества и недостатки. Преимуществом первой концепции является возможность непосредственной замены, а недостатком - увеличение числа первичных символов знаком равенства по определению. В свою очередь, преимуществом второй концепции является возможность записи дефиниции в языке системы, а недостатком - отсутствие непосредственной замены сторон дефинитивной эквивалентности. Лукасевич предлагает новый подход к определению, который должен соединить достоинства упомянутых решений и одновременно избегнуть их недостатков. Лукасевич рассматривает формулу Прототетики Лесьневского

 (2)      CEpqCfpfq.

Эта формула выражает тезис экстенсиональности, который в свободной формулировке говорит, что, если p и q эквивалентны, то сказанное о p относится также и к q. Обозначим через x и y два пропозициональных выражения, одно из которых, безразлично какое, является в определении дефиниенсом, а другое - дефиниендумом, причем каждое из них не содержит f. Полагая дефиницию истинной, принимаем формулу

(3)       Exy.

 Из (2) и (3) получаем

(4)        Cfxfy.

Воспользовавшись законом тождества Epp подставим x вместо переменной p, а к (4) применим подстановку с апострофом f/Ex’. Получим Exx и CExxExy, а после отделения - Exy. Таким образом, оказывается, что (3) равносильно (4), и поскольку (3) выше принималось в качестве дефиниции, то с таким же успехом (4) можно считать схемой дефиниции. Основным достоинством такого представления дефиниции является возможность ее записи при помощи знака импликации, а тем самым - наиболее естественного функтора исчисления высказываний. Действие (4) как схемы дефиниций поясняет пример определения отрицания в пропозициональном исчислении, основанном на импликации и константе "ложь"(0). Используя (4) запишем это определение в виде

 (5)         CfNpfCp0.

Дальнейшие шаги представляет следующий вывод:

(6)         СfpCfNpfq  (предложение Прототетики)

             (5) f/CfpCf ’fq * C(6)-(7)

(7)         CfpCfCp0fq.

Таким образом, Np (дефиниендум в (5)) оказалось замененным Cp0 (дефиниенс в (5)). Обратная замена требует доказательства импликации, обратной к (5), т.е. импликации CfCpf0Np. Ее доказательство имеет вид

(4)              Cfxfy       (схема дефиниции)

                   (4) f/Cf'fx * (8)

(8)              CCfxfxCfyfx

                   (4) f/CCfxf'Cfyfx * (9)

(9)               CCCfxfxCfyfxCCfxfyCfyfx

                    (9) * C(8)-(4)-(10)

(10)              Cfyfx

Итак, в (4) как посылка, так и заключение могут выполнять роль дефиниенса и дефиниендума. Приведенное доказательство показывает насколько логически сильным оказывается правило подстановки с апострофом, что позволяет по-новому посмотреть на определения в логических системах. [19] Вместе с тем оказывается, что роль переменных функторов от пропозициональных аргументов шире, нежели вопросы теории определений. В частности, иначе открывается перспектива аксиоматизации исчисления высказываний. В пропозициональном исчислении с переменными функторами доказуема формула

(11)         Cf0CfC00fp,

которая может быть прочитана следующим образом: если что-либо истинно о тождественно ложном предложении, и то же истинно для тождественно истинного предложения, то это же верно и для любого предложения. Поэтому Лукасевич (11) трактует как принцип двузначности, поскольку это предложение говорит, что существуют предложения истинные или ложные и только такие предложения. Вместе с тем Лукасевич высказывает мнение, что из (11) следуют аксиомы импликативно-негативного исчисления высказываний; именно эту роль и выполняет формула CfC00Cf0fp. Ученик Лукасевича, Мередит, показал, что все законы обычного исчисления высказываний, а также законы исчисления высказываний с кванторами и переменными функторами содержатся в 6-и буквенной формуле Cff0fp [1951]; эта формула по свидетельству Собоцинского была известна Лукасевичу. В этой связи Лукасевич писал следующее: "Вывод из этой формулы всего исчисления высказываний при помощи правила подстановки, правила отделения и правил для кванторов следует признать шедевром дедуктивного искусства".[20]

§ 5. Натуральный вывод Ст. Яськовского.

В 1926 г. Лукасевич поставил проблему, истоки которой можно заметить в рассмотренной выше работе "О науке". А именно, в математических доказательствах не используются логические формулы, но в них обращаются к предпосылкам и правилам рассуждений. Можно ли эти методы доказательства отобразить в системе структурных правил и исследовать их отношение к утверждениям аксиоматического исчисления высказываний? В 1927 г. Яськовский ответил на этот вопрос; результаты изложены в работе "О правилах допущений в формальной логике[1934].

 Вначале Яськовский приводит примеры, с помощью которых выясняет интуитивный смысл метода допущений. Если мы хотим убедиться в истинности формулы CpCCpqq, то можно это сделать следующим образом:

 1. Допустим p.

 2. Допустим Cpq.

 3. Из 1 и 2 следует q.

 4. С учетом того, что q есть следствие допущения Cpq получим импликацию Cpqq.

 5. С учетом допущения p получаем выражение CpCpqq.

Приведенный неформальный вывод кодируется следующим образом:

 1.Sp

 1.1.SCpq

 1.1.q

 1.CCpqq

  CpCCpqq

Символ S является сокращением для оборота "допускается". Каждое допущение предваряет цифровой префикс. Префикс, составленный из одной цифры и точки означает главное допущение в данном выводе, а префикс, составленный из большего числа цифр и точек, означает дальнейшие допущения. Если последующее допущение обозначено префиксом, начальный сегмент которого идентичен с префиксом некоторого уже записанного в данном выводе допущения, то это значит, что мы имеем дело с допущением, охватываемом предыдущим допущением, например, SCpq находится, если можно так выразиться, в области допущения Sp. Если строка вывода предваряется цифровым префиксом, после которого знак S не записывается, то тогда выражение, стоящее непосредственно после префикса, является следствием допущения, имеющего тот же префикс, например, q является следствием SCpq.

Яськовский представляет систему натуральной дедукции в виде последовательности выражений, каждое из которых он считает принадлежащим исчислению. В частности, предполагается, что истинными формулами системы являются допущения и их следствия. Столь широкое понимание истинной формулы, конечно, не противоречит ее пониманию в узком смысле как формулы доказуемой.

 Описание системы начинается приведенным выше примером и Яськовский предполагает, что к моменту написания первого допущения никакие прочие формулы не существуют. Если какая-либо формула T имеет номер n, то все формулы, имеющие в начальном сегменте номер n, принадлежат (вместе с T) к области T; в приведенном примере к области формулы q принадлежат выражения Sp, SCpq и само q. Под абсолютной областью Яськовский понимает множество всех записанных формул системы, а сама абсолютная область увеличивается одновременно с развитием всей системы. К моменту написания первой формулы абсолютная область представляет собой пустое множество. Эти свойства пополнения формальной системы свидетельствуют о влиянии Лесьневского. В 1926 г. на семинаре Лукасевича понятие области Яськовский эксплицировал следующим образом:

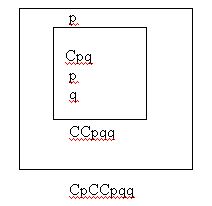
Однако префиксная нотация областей допущений в качестве их имен противоречит взглядам Лесьневского. В этой связи Яськовский замечает: "Можно понимать область как класс выражений в согласии со взглядами Лесьневского на класс как материальный объект, но в этом случае толкование сегментов будет модифицировано и формулировка правил тем самым значительно усложниться". ([1934], S.9)

 Правила построения системы Яськовского следующие:

(R1) К каждой области формул D можно добавить выражения, состоящие из (a) префикса, который отличен от начального сегмента префикса произвольного элемента D, (b) точки, (c) символа S, (d) предложения.

(RII) Если в области D допущения x истинным является предложение y, то к области, в которой D является подобластью, можно добавить предложение Cxy. Из двух областей D и D`, где D - область допущения x, а D` - абсолютная область или область допущения x`, префикс которой идентичен с начальным сегментом префикса допущения x, D является подобластью D` и D есть непосредственная подобласть D` тогда и только тогда, когда D не является подобластью никакой подобласти D`.

 (RIII) Если в данной области D истинны предложения Cxy и x, то допустимо к D добавить y; это правило, конечно, является правилом modus ponens для естественного вывода.

 (RIV) Если в области D допущения Nx истинны предложения y и Ny, то к области, относительно которой D является подобластью, можно добавить предложение x.

 Используя приведенные правила Яськовский конструирует систему, содержащую 59 предложений "теории дедукции" (в выводе обозначаемых td); ниже приводятся первые двадцать из них (с правой стороны даны номера предложений и правил, используемых в выводе данного предложения:

td1              1.Sp                                                       I

td2              1.1.SCpq                                                I

td3              1.1.q                                                      III,2,1

td4              1.CCpqq                                                II,2,3

td5              CpCCpqq                                               II,1,4

td6              2.SCNpNq                                              I

td7              2.1.Sq                                                     I

td8              2.1.1.SNp                                               I

td9              2.1.1.Nq                                                 III,6,8

td10             2.1.p                                                      IV,8,7,9

td11             2.Cqp                                                    II,7,10

td12             CCNpNqCqp                                         II,6,11

td13             1.2.Sq                                                    I

td14             1.Cqp                                                    II,13,1

td15             CpCqp                                                   II,1,14

td16             1.3.SNp                                                 I

td17             1.3.1.SNq                                              I

td18             1.3.q                                                      IV,17,1,16

td19             1.CNpq                                                  II,16,18

td20             CpCNpq                                                 II,1,19

Таким образом, система вывода Яськовского строится на допущениях и правилах вывода, но ее отличие от генценовской системы помимо кодификационных особенностей, определяемых, вероятно, бесскобочной записью, состоит и в том, что она сохраняет подобласти абсолютной области (означаемой по мере построения формулами без префиксов) и тем самым содержит также правила построения всей системы. Итак, утверждения логики в системе Яськовского не предваряют цифровые префиксы. Он формулирует метатеорему, утверждающую эквивалентность аксиоматической системы Лукасевича и системы, построенной на допущениях. "Доказательство" этого утверждения является в сущности лишь абрисом проблемы и покоится на понятии построения предложения, центральное значение которого передается термином "эквиморфный" (equiform).

Несомненно, конструкция Яськовского принадлежит к наиболее выдающимся достижениям, полученным не только семинаре Лукасевича, но и во Львовско-варшавской школе. Если учесть, что первые результаты датируются 1926 г., то система польского логика является первой системой естественного вывода в логической практике.

                                            § 6. Метаматематические исследования логики.

Обзор развития логических исследований в школе (классического пропозиционального исчисления; неклассическим логикам будет посвящен отдельный параграф) закончим кратким абрисом, в центре которого находится работа Лукасевича и Тарского[1930] "Исследования исчисления предложений", называемой авторами в тексте также и "сообщением". Цель этого сообщения состояла в подытоживании фактов, "касающихся [...] "метаматематики", или - лучше - "металогики"".

Первые результаты из области металогики относятся к 1924 г. В сообщении Лукасевича [1925] (еще без доказательства) утверждается, что аксиомы исчисления высказываний в Principia Mathematica Рассела и Уайтхеда, а также аксиомы, приведенные Гильбертом, как и аксиомы самого Лукасевича, изложенные выше, не являются независимыми. В частности, Лукасевич показал, что аксиому CApAqrAqApr можно вывести из аксиом CAppp, CqApq, CApqAqp и CCqrCApqApr (Principia), а аксиому CCpCpqCpq - из аксиом CpCqp, CCpCqrCqCpr, CCqrCCpqCpr, CpCNpq, CCpqCCNpqq (Гильберт).[21] Позже Лукасевич [1929],[1934] показал, что и аксиомы Фреге также не являются независимыми. Систематическое изложение результатов дано в курсе лекций Лукасевича [1929]. Годом позже в сообщении Лукасевича и Тарского "Исследования исчисления высказываний" [1930] подведены итоги работы семинара, в котором, начиная с 1926 г. получили результаты авторы статьи, а также Вайсберг, Собоцинский и Линденбаум.

Для доказательства независимости аксиом исчисления высказываний Лукасевич применил многозначную матрицу, идея которой принадлежит Тарскому. Этот метод очевидным образом соотносится с развернувшимися в Варшаве исследованиями многозначных логик, приведших к созданию логических матриц, отличных от двузначных.[22] Лукасевич [1929] и Вайсберг [1937] разработали также оригинальные методы доказательства полноты исчисления высказываний в смысле Поста.

Остановимся подробнее на неоднократно упоминаемом "сообщении" Лукасевича и Тарского, центральным понятием которого является множество S всех предложений данного исчисления высказываний и понятие логической матрицы. Множество S определяется как пересечение всех множеств, содержащих пропозициональные переменные и замкнутое относительно операций образования составных предложений. В случае импликативно-негативного исчисления - это операции импликации и отрицания. Если X содержится в S, то Cn(X) - это множество следствий множества X, являющееся пересечением всех множеств, содержащих X и замкнутых относительно правил, определяющих операции в Cn; в случае исчисления высказываний это правила операций подстановки и отделения. В этой конструкции впервые для определения металогических понятий (множества предложений, следствия) использована конструкция наименьшего множества, замкнутого относительно определенных в нем операций.

Другим важным понятием сообщения является понятие логической матрицы, определяемое как упорядоченная четверка M=<A,B,f.g>, где A и B - дизъюнктные множества произвольных элементов, f -двух-, а g - одноаргументные функции, определенные для всех элементов множества A+B и принимающие значения из него. M является нормальной матрицей, если из того, что xÎ B и yÎ A следует, что f(x,y) Î A. Функция h называется функцией оценки матрицы M, если выполняются следующие условия:

1) функция h определена для каждого xÎ S;

2) если x есть пропозициональная переменная, то h(x)Î A+B;

3) если x,yÎ S, то h(c(x,y))=f(h(x),h(y));

4) если xÎ S, то h(n(x))=g(h(x). Предложение x удовлетворяет матрице M, если для каждого значения функции h этой матрицы имеет место h(x)Î B, а элементы множества B называются выделенными.

Рассмотрим матрицу M=<{0},{1},f,g>, где функции f и g определены следующим образом: f(x,y)=1, когда x=0, y=1, или x=1, y=1, или x=0, y=0 и f(x,y)=0, когда x=1, y=0, а g(x)=1, когда x=0, g(x)=0, когда x=1. Множества {0} и {1} дизьюнктны, а 1 является выделенным значением. Функции f и g определены на истинностных значениях. Легко видеть, что существует функция оценки h, согласованная с таблицами истинности для импликации и отрицания; символы c и n при определении функции h являются метаязыковыми именами C и N. Матрица M, очевидно, является нормальной матрицей. Таким образом, установлено соответствие между алгеброй истинностных оценок и алгеброй предложений. Более того, поскольку элементы множества A и B могут быть произвольной природы, то Линденбаум предложил таковыми считать предложения и матрица в этом случае становится алгеброй Линденбаума. Очевидно, что произвольное предложение исчисления высказываний удовлетворяет матрице, т.е. такое предложение оценивается как истинное. Тем самым можно отождествить множество истинностных предложений с предложениями, выполняемыми на матрице. Обозначим это множество E(M).

Далее, в сообщении приводится два важных утверждения, устанавливающие зависимость между предложениями исчисления и содержанием матрицы. Утверждение 1. Если M является нормальной матрицей, то E(M) - дедуктивная система, т.е. система, содержащая свои следствия. Утверждение 2. Если X - дедуктивная система, то существует нормальная матрица M, для которой множество A+B конечно, перечислимо и выполняется соотношение E(M)=X. Эти утверждения, особенно второе, оказались весьма важными, ибо матрица попросту определяет негативно-импликативное исчисление высказываний, а из этой дефиниции легко можно показать, что исчисление высказываний непротиворечиво и полно.

Дальнейшее обсуждение сообщения Лукасевича и Тарского будет продолжено в следующем параграфе, т.к. касается логик неклассических. Здесь же, в завершение, упомянем интересные металогические результаты действительно демонстрирующие реализацию лозунга "логика для логики". Так Собоцинский показал, что исчисление высказываний, содержащее формулы CpCqp и CpCqCCpCqrr, для каждого натурального n обладает аксиоматическим базисом, насчитывающим в точности n элементов, а Тарский обобщил это утверждение для произвольного пропозиционального исчисления. Вайсбергом доказано следующее утверждение: в исчислении высказываний (функционально полном или частичном), содержащим формулу CpCqCrp, аксиомы содержат как минимум три различные пропозициональные переменные. Несколько отступающим от лозунга школы является следующая находка Тарского, позволяющая определить функтор отрицания при помощи универсального квантора (Np=CpПp). Этот результат послужил основанием для конструкции расширенного исчисления высказываний (Лукасевич, Тарский [1930]).

Глава 2.  Ян ЛукасевиЧ и неклассиЧеские логики.

 

§ 1.  М ногозначные логики

Хорошо известно, неклассическая логика - это необязательно логика двух истинностных значений - истины и лжи; неклассичность определяется семантикой логических связок, или, если последнее понятие понимать шире - семантикой логических операторов. Внешним выражением сказанного как раз и является бесскобочная запись. По этой причине в настоящем параграфе будут обсуждены логические исчисления, относящиеся к неклассическим также и традиционно: многозначные логики, модальные логики, интуиционистское исчисление высказываний, а также упомянута дискуссионная логика Яськовского. Появление этих  систем  во Львовско-варшавской школе также неотделимо от имени Лукасевича. Ранее уже высказывалась мнение, обозначившее роль философа Лукасевича в логике и сводившееся к тому, что он был в логике метафизиком. В этой связи была затронута работа "Об индукции как инверсии дедукции", которая вместе с другими ранними работами при рассмотрении истоков многозначной логики, как правило, не учитывалась. Обычно считается, что первое упоминание о многозначной логике было сделано Лукасевичем 7 марта 1918 г. в прощальной лекции перед уходом на работу в Министерство вероисповеданий и публичного просвещения[23]. У этого сообщения имеется предыстория, отражающая эволюцию философа Лукасевича в направлении к логике, начало которой было положено рядом работ, сформировавших парадигму философии предложения этого исследователя. В кратком обзоре генезиса взглядов "раннего" Лукасевича мы коснемся некоторых из них.

Существовала да и существует до сих пор тенденция связывать индукцию с вероятностным подходом или, как его называли ранее, особенно логики, с правдоподобием. Вначале Лукасевич был сторонником т.н. инверсной теории дедукции, согласно которой индукция является рассуждением, в котором отыскивается логическое основание для единичных предложений опыта. Связь индуктивных и дедуктивных рассуждений он обобщил, следуя Твардовскому, в понятии рассуждения как процесса. Лукасевич [1912],[1915] различает основание и следствие, которые не соответствуют паре посылка-заключение, и в связи с этим вводит направление рассуждения. Если посылка является основанием, а заключение - следствием, то речь идет о дедуктивном рассуждении, а если посылка есть следствие, а заключение - основание, то речь идет о рассуждении-редукции, или говоря иначе, дедукция является нахождением следствия по данному основанию, а редукция - основания для данного следствия. Дедукция является надежным, безошибочным рассуждением, тогда как редукция - всего лишь правдоподобным. Но в [1909] Лукасевич, анализируя формулу Лапласа p=n+1/n+2, по которой определяется правдоподобие того, что n+1 событие обладает свойством, которое проявилось в n событиях, формулирует аргумент, ставивший под сомнение осмысленность приписывания индуктивным заключениям меры правдоподобия. Формула Лапласа касается единичного события, тогда как в индуктивном заключении речь идет о правдоподобии генерализации. Можно воспользоваться т.н. обобщенной формулой Лапласа p=n+1/n+m+1, где m - это число событий, охваченных генерализацией, а n - базис индукции (число наблюдаемых событий). Поскольку m много больше n, то p не может быть больше 1/2, а если m стремится к бесконечности, то p - к нулю.[24] Поэтому Лукасевич в работе "Логические основания исчисления правдоподобия"[1913] старается выяснить, почему понятие правдоподобия не относится к предложениям (суждениям). Он считает, что меру правдоподобия можно приписывать пропозициональным функциям в виде отношения числа аргументов, для которых она истинна, к конечному числу всех значений переменной. Предложения, т.е. формулы без свободных переменных бывают или истинными, или ложными и понятие правдоподобия к ним не относится вообще.

Таким образом, если истинностную оценку считать именем предложения в косвенном употреблении, то, очевидно, отождествить ее с ситуацией невозможно. Поэтому Лукасевич оставляет индукцию как опосредующий метод, предваряющий дедукцию и обращается непосредственно к ревизии рассуждения как понятию, охватывающему и индукцию, и дедукцию. Эта ревизия состояла в высказывании сомнения относительно универсальности двух важнейших законов: принципа исключенного третьего и принципа противоречия. Если второму из этих законов посвящена монография "О принципе противоречия у Аристотеля"[1910], то о первом можно найти упоминание в коротком отчете "О принципе исключенного среднего"[1910a]. Исходная позиция метафизика Лукасевича в ревизии обоих этих законов одна. В отчете он пишет: "[...] два важнейших онтологических принципа, известных как принцип противоречия и принцип исключенного среднего истинными сами по себе не являются, но требуют доказательства; однако поскольку доказать их не удается, особенно в применении к реальным предметам, то их следует считать только допущениями. Поэтому необходимость признания этих принципов не имеет логического источника, но проистекает из определенных практических потребностей"(S.126).

В ревизии рассуждения как процесса, в частности, процесса приписывания свойств предметам именно последние стали для Лукасевича на какое-то время целью анализа, и здесь можно обнаружить выразительное влияние А.Мейнонга, в семинарах которого в 1909 г. в Граце участвовал Лукасевич. В выводах упомянутого отчета он ставит под сомнение, "подпадают ли под принцип исключенного среднего общие предметы, такие как треугольник вообще, человек вообще и т.д." "Но если речь идет о реальных предметах,- продолжает Лукасевич - принцип исключенного среднего, кажется, остается в тесной связи с постулатом повсеместной детерминации явлений, не только теперешних и прошедших, но и будущих". ([1910a], S.126-127)

Оба упомянутых принципа для Лукасевича являются ничем иным, как способом рассуждения, процессом, правильность которого не может приниматься "на веру". В "Принципе противоречия" он не приступает к анализу этого закона с априористских позиций, считая, что "все же плохо, когда в философии существуют неприкасаемые принципы; хуже, если эти принципы не обоснованы; еще хуже, если эти неприкасаемые и необоснованные принципы когда-то были предметом ожесточенного спора. Как же получилось, что спорный принцип, которого никто не умеет доказать, считается настолько правильным, что и коснуться его даже невозможно? Куда же подделась научная критика, которой мы так гордимся в эпоху критицизма?" ([1910], S.6) Поэтому Лукасевич считает для себя невозможным аксиоматически принять принцип противоречия, особенно после того, как тот стал предметом спора, который он лишь упоминает, не приводя впрочем аргументов "за" и "против". По поводу Гегеля, также являющегося противником принципа противоречия, а значит в какой-то мере также ревизовавшем этот принцип, Лукасевич пишет:" Гегель [...] создал "метафизическую логику", не основывающуюся на принципе противоречия. Но эта попытка была чересчур радикальной, нечеткой и неясной, чтобы быть понятой и принятой".(S.5) И поскольку этот принцип оказался необоснованным Лукасевич приступает к его анализу.

Работа Лукасевича состоит из двух частей: исторической и систематической. В первой он различает три аспекта принципа противоречия: онтологический, логический и психологический.

Онтологический принцип противоречия: ни один предмет не может одновременно обладать и не обладать одним и тем же свойством.

Логический принцип противоречия: два суждения, в одном из которых предмету приписывается некоторое свойство, а в другом это свойство отрицается, не могут быть одновременно истинными.

Психологический принцип противоречия: два убеждения, которым соответствуют два противоречивых суждения, не могут существовать в одном сознании.

Затем Лукасевич показывает, что хотя онтологическая и логическая формулировки принципа не равнозначны, но для Аристотеля они тождественны. Лукасевич согласен с этим взглядом Стагирита и в дальнейшем пользуется обоими формулировками взаимозаменяемо. Что же касается психологической формулировки, то ее Лукасевич считает эмпирическим принципом, а поэтому доказательство закона противоречия на основании априорных суждений, к которым относятся также онтологическая и логическая формулировки, невозможно. Критика психологического принципа противоречия как логического закона является первым аргументом Лукасевича, ставившего под сомнение правильность воззрений Аристотеля на этот принцип. Вторым аргументом, вызвавшем сомнение Лукасевича, служит тезис, что можно найти более очевидный и простой принцип, нежели принцип противоречия и таковым польский логик считает принцип тождества. Вместе с тем - и это главный упрек Аристотелю - Стагирит не является последовательным, поскольку, с одной стороны, он считает, что принцип противоречия недоказуем, а с другой - формулирует ряд его доказательств. По мнению Лукасевича все доказательства (главным образом апагогические) не верны с формальной точки зрения. Лукасевич считает, что непоследовательность Аристотеля можно объяснить психологическими мотивами: "Кажется, никто не чувствовал сильнее необходимость доказательства принципа противоречия, чем сам Аристотель; однако он не умел и не мог согласиться с этим чувством убеждения, что принцип противоречия как принцип окончательный не может быть доказан. Тем самым он оказался в неудобном положении: запутался в противоречиях в самом рассмотрении принципа противоречия". ([1910], S.51-52)

Прочие возражения Лукасевича могут быть сведены к следующим положениям: а) принцип противоречия как закон логики не является ни достаточным, ни необходимым, ибо можно рассуждать дедуктивно или индуктивно и делать это непротиворечиво; б) принцип противоречия не удается вывести из дефиниции истины или лжи, как не удается его вывести ни из принципа тождества, ни из принципа двойного отрицания; в) можно привести формальное доказательство принципа противоречия, используя определение предмета как чего-то, что не обладает противоречивыми свойствами, однако это доказательство будет формальным, а не предметным. Так как для доказательства принципа противоречия нужно предварительно показать, что ни один предмет не является противоречивым, в чем Лукасевич весьма сомневается, то свою монографию он заканчивает словами: "Поскольку принцип противоречия предметно не удается доказать, несмотря на то, что такое доказательство необходимо, то он не имеет логической ценности. Зато он имеет важную практическо-этическую ценность, будучи единственной защитой против ошибок и лжи.- Поэтому мы должны его принять" ([1910],S.152)

Таким образом оказывается, что для Лукасевича логическое основание не является единственным и даже важнейшим мотивом в решении принятия тех или иных суждений: свойство истинности суждения переводится в этическую плоскость, как потом окажется, единственно с целью освободиться от формальных ограничений, а тем самым и от самого принципа противоречия. В данном случае этические мотивы сыграли роль метатеории.[25]

И наконец следует ответить на вопрос: какую роль сыграла монография "О принципе противоречия у Аристотеля" в процессе формирования идеи многозначной логики? На первый взгляд влияние этой работы может показаться минимальным, поскольку о ней Лукасевич почти не вспоминает в своем дальнейшем творчестве[26]. Одно из таких упоминаний можно обнаружить в статье "О творчестве в науке", где в примечании Лукасевич высказывает неуверенность в применении этого принципа к реальным предметам. Более существенное упоминание содержится в прощальной речи от 7 марта 1918 г. В ней Лукасевич впервые публично без подробностей заявил о сконструированной им системе трехзначной логики, а при случае вспомнил, что уже в "Принципе противоречия" старался показать, что этот принцип не очевиден, и что в это время (т.е. около 1910 г.) он пробовал сформулировать неаристотелевскую логику, но попытки эти не увенчались успехом. Упоминания об этой книжке нет даже в исследовании, посвященном силлогистике Аристотеля, хотя может показаться, что обе эти работы служат как бы началом и окончанием его творчества в области истории философии и логики. Можно предположить, что Лукасевич занял позицию, подобную той, что и Лесьневский в своем отступничестве, руководствуясь аналогичными мотивами, а именно, он считал, что работа "О принципе противоречия у Аристотеля" является метафизической, чрезмерно отягощающей логику онтологией. Ведь в "логическом" периоде Лукасевич разделял совершенно иные взгляды на отношение логики и онтологии. Когда он сформулировал систему многозначной логики, то считал, что опыт может и должен решить, какая логика является формальной моделью мира. Еще позже, в период II мировой войны, Лукасевич склонялся ко взгляду, что выбор логики является делом конвенции. Таким образом, очевидного повода возвращаться к своей первой книжке у Лукасевича не было. Тем более позже оказалось, что с точки зрения многозначной логики исторически более интересными были взгляды Аристотеля на принцип исключенного третьего, нежели на принцип противоречия. И все же следует признать, что ревизионистские интенции Лукасевича мало зависели от объекта исследования и были направлены на метод рассуждения. Логические законы были единственно поводом для обнаружения границ уверенности логических рассуждений. Лукасевич пишет: "Должен наступить момент, когда логики начнут рассматривать взаимные отношения этих принципов (т.е. принципов логики, в т.ч. принципа противоречия.- Б.Д.). [...] Лишь тогда окажется, какое место среди логических законов занимает принцип противоречия, в чем состоит его правильность и ценность, как далеко простирается действенность его применения; тогда окажется, действительно ли этот принцип важнейший из всех и является ли он краеугольным камнем всей нашей логики, или же его можно преобразовать, а даже опустить и создать систему неаристотелевской логики так, как возникла посредством преобразования аксиомы о параллельных система неэвклидовой геометрии"(S.7-8)

Сопоставляя тексты прощальной речи 1918 г. и приведенную цитату из "Принципа противоречия" можно однозначно констатировать, что в период 1910-1918 гг. Лукасевич пробовал сконструировать неаристотелевскую логику и свое решение связывал с ревизией принципа противоречия. И хотя в "Принципе противоречия" XVI глава носит название "Неаристотелевская логика", она не содержит ничего, кроме методологических рассуждений о значимости этого принципа. Таким образом, удостоверившись в логической недоказуемости принципа противоречия и в значимости его этической и практической аргументации Лукасевич как бы возвращается к упомянутому выше отчету "О принципе исключенного среднего", а в сущности возвращается к метафизическим основаниям процесса рассуждения - к вопросу о необходимости логических законов. Правда, эту необходимость он узрел в онтологии, что и позволило ему закон исключенного среднего считать не логическим законом, а металогическим. Оказалось, что неаристотелевская логика требует ревизии принципа двузначности: каждое предложение является или истинным, или ложным. Пересмотр этого принципа Лукасевич совершил в известной работе "О детерминизме", являющейся его ректорской речью в 1922/23 учебном году. Он пишет: "Именно потому этот принцип и не может быть доказан, что он лежит в основании логики. В него можно только поверить, а поверит в него тот, кому он покажется очевидным. Тогда я могу этот принцип не признавать и принять, что наряду с истинностью и ложностью существуют иные логические оценки, по крайней мере еще одна, третья логическая оценка". ([1922], S.125) Комментируя высказывания Аристотеля о будущих случайных событиях (известная проблема морского боя) Лукасевич приходит к выводу, что Стагирит сомневался в универсальности принципа исключенного среднего, тогда как решительным сторонником двузначности были стоики во главе с Хрисиппом. Поэтому Лукасевич называет новую, трехзначную логику не неаристотелевской, а нехрисипповой.

Но прежде чем коснуться этой знаменитой работы отметим резонанс в философской среде, вызванный монографией "О принципе противоречия у Аристотеля". Попросту говоря, на страницах журнала "Пшегленд филозофичны" возникла дискуссия. Так Лесьневский[1912] присоединился к взгляду, что принцип противоречия требует доказательства и предложил таковое, носящее онтологический характер. У Котарбинского [1913a], в свою очередь, сомнение вызвал принцип исключенного третьего и он предложил, что наряду с предложениями ложными и истинными могут существовать неопределенные предложения, т.е. такие, которые сегодня ни истинны, ни ложны, например, предложение "завтра я пойду гулять".[27] Неопределенные предложения связаны с фактами, создаваемыми в будущем человеческой деятельностью, а их истинность вечна, но не предвечна. Отсюда, по мнению Котарбинского, ни одно суждение не может быть одновременно истинным и ложным (принцип противоречия). И вместе с тем невозможно, чтобы некое суждение не было истинным, а его отрицание было ложным, и если данное суждение не было ложным, то его отрицание было истинным, поскольку значим закон: для каждого суждения p, p истинно, либо p неистинно, или p ложно, либо p не ложно; по мнению Котарбинского последнее утверждение является ослаблением закона исключенного среднего.[28] Лесьневский [1913a] приводил аргументы в защиту тезиса, что каждая истина не только вечна, но и предвечна, а в [1913] он ставил под сомнение закон исключенного среднего. По мнению Лесьневского существуют пары предложений, которые будучи взаимными отрицаниями, являются ложными, например, "квадратный круг есть круг" и "неправда, что квадратный круг есть круг". Но Лесьневский, вопреки Котарбинскому, защищает принцип двузначности.[29] К проблемам, затронутым в "Принципе противоречия у Аристотеля" Лукасевич вернулся только в 1918 г. в упоминавшейся выше речи и в двух коротких рефератах "О понятии возможности" [1920] и "О трехзначной логике" [1920a].

Таким образом, в двадцатые годы принцип двузначности в размышлениях Лукасевича занял место принципа противоречия. Оба этих закона не могут быть доказаны и получают поэтому статус принципов, но в отличие от принципа двузначности принцип исключенного третьего не требует защиты в виде аргументов практического и этического характера, поскольку оказалось, что введение в рассмотрение более двух истинностных оценок позволяет последовательно строить логическую систему. Но наиболее значимое различие этих принципов в [1910] и последующих работах Лукасевича состояло в том, что принцип противоречия трактовался как обычный логический закон, а принцип двузначности - как закон металогический. Поэтому оказалось, что конструкция нехрисипповой логики зависит не столько от набора аксиом, сколько от решения метатеоретических вопросов, ибо когда Лукасевич писал "Принцип противоречия" он не различал логику и металогику. Сомнению подвергался логический закон (принцип противоречия) и нет ничего удивительного в том, что он получил в результате фрагмент классической логики, а не новую, неаристотелевскую логику.

Значения принципа двузначности было позже выяснено в исследованиях Лукасевича, Лесьневского и Тарского. В обычном исчислении высказываний принцип двузначности сформулировать не удается. Но в более богатых логических системах, например, в Прототетике Лесьневского или в исчислении высказываний с переменными функторами принцип двузначности является теоремой. Если в таких системах принято стандартное определение конъюнкции, дизъюнкции и отрицания, то следствием принципа двузначности будут законы противоречия и исключенного среднего. Например, без принятия того, что отрицание истинного предложения ложно, а отрицание ложного предложения истинно, с принципом двузначности согласуется предложение "два взаимно отрицающих друг друга предложения могут быть одновременно ложными"; это предложение согласуется с принципом двузначности до тех пор, покамест не будет принято, что конъюнкция двух ложных высказываний - ложна.[30]

Возвращаясь к "семантике" трехзначной логики, т.е. к проблеме детерминизма отметим, что Лукасевич полагал, будто из принципа двузначности следует принцип детерминизма, но не наоборот, и подобное же соотношение имеет место между принципом трехзначности и принципом индетерминизма, причем под индетерминизмом Лукасевич понимал взгляд, согласно которому в будущем относительно момента t могут возникнуть события, не предрешенные в момент t. Предрешить же значение самой "неаристотелевской логики" Лукасевич не берется, констатируя единственно значение теоретическое, т.е. как удавшуюся ревизию теоретического метода рассуждения. А поскольку семантика такой логики не была прояснена, то и практическое ее значение остается невыясненным, но имеющим для Лукасевича несомненную ценность. Он пишет: "Будет ли и какое практическое значение иметь новая система логики - это выяснится лишь тогда, когда в свете новых логических законов окажутся проведенные подробные исследования логических явлений, особенно имеющих место в дедуктивных науках и когда можно будет сравнить с опытом следствия индетерминистского взгляда на мир, являющегося метафизическим основанием новой логики".([1920] ,S.131)

В 1922 г. Лукасевич обобщил трехзначное исчисление высказываний до логики, имеющей произвольное конечное число истинностных оценок. Значение импликации и отрицания определялось в нем следующими соотношениями: Cpq=1, для p£ q, Cpq=1-p+q, для p> q, Np=1- p, где 0< p, q<1. Если же из отрезка [0,1] использовать только крайние значения, то получается случай двузначной логики. Говоря обобщенно, приведенные соотношения определяют произвольное многозначное исчисление высказываний L_n, где n - произвольное натуральное число не меньше 2; L₂ - это просто двузначное исчисление высказываний. Тавтологией произвольного L_n-исчисления (для фиксированного n) является формула, принимающая значение 1 для произвольного набора значений пропозициональных переменных. Следующим шагом в обобщении многозначной логики было принятие в качестве истинностных значений бесконечного числа оценок, хотя и перечислимого. В такой системе L_À соотношения для C и N такие же, как в L_n. Таким образом, возникает последовательность исчислений от L₂ до L_À , причем все L_n (n>2) содержится в L₂, т.е. все тавтологии всех L_n строго включаются в L₂. Для L_n и L_m (n<m) Линденбаум (Лукасевич, Тарский[1930]) показал, что L_m содержится в L_n, если n-1 является делителем m-1. L_À содержится во всех конечнозначных L_n.

До сих пор речь шла о матричной конструкции многозначной логик. Естественно, в Школе попытались эти исчисления аксиоматизировать. Вайсберг [1931] доказал, что L₃ аксиоматизируется следующими формулами: CpCqp, CCpqCCqrCpr, CCNpNqCqp, CCCpNppp; правилами вывода являются подстановка и отделение. Тот же автор высказал гипотезу (Лукасевич, Тарский[1930]), которую позже и доказал [1935], что каждое конечнозначное исчисление L_n аксиоматизируемо, если оно содержит следующие формулы: CCpqCCqrCpr, CCqrCCpqCpr, CCqrCpp, CCpqCNqNp, CNqCCpqNp. Лукасевич высказал гипотезу, что L_x аксиоматизируется выражениями CpCqp, CCpqCCqrCpr, CCCpqqCCqpp, CCCpqCqpCqp, CCNpNqCpq.[31]

Все приведенные аксиоматики оказались неполны в том смысле, что первичных терминов C и N оказалось недостаточно, чтобы определить все функторы многозначного исчисления высказываний, причем для каждого L_n (n>2). Дело в том, что число функций стремительно растет с ростом n и, например, для n=3 число одноаргументных функций равно 27, а функций от двух аргументов - 19683. Слупецкий [1936] решил проблему функциональной полноты для L₃. Он определил одноаргументный функтор T такой, что Tx = 1/2 для произвольного x Î {0, 1/2, 1}. Функторы C, N, T определяют все функторы исчисления L₃. Чтобы получить аксиоматику L₃ нужно к приведенным выше аксиомам Вайсберга добавить формулы CTpNTp, CNTpTp.

Все исчисления L_n (n> 1) непротиворечивы. Сложнее обстоит дело с полнотой. Полноту L₃ доказал Слупецкий [1939],[1946]. В связи с исследованиями функции T и вопросом полноты (каждая тавтология принадлежит системе) Слупецкий [1939a] сформулировал простой критерий функциональной полноты для произвольного L_n: многозначное исчисление высказываний функционально полно, если первичные термины этой системы позволяют определить каждый одноаргументный функтор, и когда по меньшей мере один из первичных терминов этого исчисления, являющийся функтором двух аргументов, определяется истинностнозначной матрицей со следующими свойствами: а) не все строки внутренней части таблицы идентичны, б) не являются идентичными все столбцы таблицы, в) во внутренней части таблицы должны находиться все значения, которые могут принять аргументы функторов этого исчисления. Приведенные требования носят название критерия Слупецкого.[32] Обсуждаемые выше исчисления были системами с одним выделенным значением. Собоцинский [1936] исследовал исчисления с двумя выделенными значениями, а Слупецкий [1939] - с k<n выделенными значениями.

В 30-е годы Лукасевич [1930] оценивал изобретение многозначных логик так: "Я сразу осознал, что среди всех многозначных систем только две могут претендовать на философскую значимость: трехзначная система и система бесконечнозначная. [...] Считаю, что именно этой последней системе принадлежит первенство среди прочих".(S.159) И далее: "Все же мне кажется, что философское значение представленных здесь систем логики может быть по меньшей мере так же велико, как и значение неэвклидовых систем геометрии".(S.161) Позже, в [1953] Лукасевич изменил свой взгляд на философскую значимость трех- и бесконечнозначной систем логики. Предлагал также Лукасевич, чтобы многозначные системы исчисления высказываний и предикатов послужили основанием для исследований в арифметике и теории множеств. Таким образом, значение этих систем для Лукасевича двоякое: философское и математическое.[33]

§ 2. Модальные логики.

Уже первые изложения трехзначной логики в 1920 г. содержали явную связь модальности и многозначности. Лукасевич считал, что в двузначной логике не удастся согласовать интуитивные трактовки модальных функторов. Эта мысль является следствием объяснения формализации модальностей не как операторов, а как функторов, уравненных концептуально в правах с логическими знаками. Это свое убеждение Лукасевич последовательно выражал на протяжении всего своего научного творчества. [34]

Первое систематическое изложение модальной логики дано Лукасевичем в работе с названием "Философские замечания о многозначных системах исчисления предложений."[1930] Правда, здесь не представлена система модальной логики как таковая, но только показаны требования, которым должна, по мнению Лукасевича, удовлетворять такая система. Модальными предложениями Лукасевич называет следующие четыре выражения:

(1) возможно, что p - символически : Mp;

(2) невозможно, что p - символически  : NMp;

(3) возможно, что не-p - символически  : MNp;

(4) невозможно, что не-p - символически  : NMNp.

Традиционные утверждения о модальностях по мнению Лукасевича можно разделить на три группы. К первой группе относятся предложения следующего вида: (a) Ab oportere ad esse valet consequentia (Если что-либо необходимо, то оно существует); (b) Ab esse ad posse valet consequentia (Если что-либо существует, то оно возможно); (с) Ab non posse ad non esse valet consequentia (Если что-либо невозможно, то оно не существует). Общим представителем этой группы является предложение

(I): Если невозможно, что p, то не-p.

Вторую группу составляет утверждение Лейбница из Теодицеи: (d) Unumquodque, quando est, oportet esse (Чтобы то ни было, когда оно существует - оно необходимо). Лукасевич замечает, что последнее высказывание в действительности происходит от Аристотеля и разбирает возможные интерпретации Стагирита. В результате анализа оказывается,  что слово "quando" в предложении (d), как и соответствующее ему "hotan" у Аристотеля,  являются частицами, выражающими не условие, но время. Однако временная форма переходит в условную форму, поскольку в связанных временными рамками предложениях определение времени оказывается включенным в содержание предложений.[35]

 Предложение (d) имеет следующую эквивалентную формулировку

(II): Если предполагается, что не-p, то невозможно, что p.

Третью группу представляет аристотелевский принцип обоюдной возможности

(III): Для некоторого p, возможно, что p, и возможно, что не-p.

В символике исчисления высказываний предложения (a)-(c) имеют вид: (1) CNMpNp, (2) CNpNMp, (3) S pKMpMNp (в последнюю формулу входит знак экзистенциального квантора). Выражения (I)-(III) Лукасевич трактует как временные аксиомы модальной логики и выводит из них при помощи обычного исчисления высказываний ряд следствий: (5) CpMp, (6) CNpMNp, (7) CNMNpp, (8) CNMNpMp, (9) CNMpMNp, (10) CMpp, (11) CMNpNp, (12) CpNMNp, (13) CMpNMNp, (14) CMNpNMp. Формулы (5)-(9) являются следствиями (I), а оставшиеся - следствиями (II). Некоторые из приведенных формул очевидны, например, (5), которая утверждает, что то, что существует, возможно. Однако другие весьма сомнительны с интуитивной точки зрения, например, (10), утверждающая, что если что-либо возможно, то оно существует. Короче говоря, следствия, полученные из (I) интуитивно прозрачнее, нежели следствия из (II). Аксиома (II) является обратной аксиоме (I). Взаимно противоположными являются формулы (5) и (10), (6) и (11), (7) и (12), (8) и (13), (9) и (14). Поэтому имеют место эквивалентности EpMp, ENpMNp, ENMNpp, ENMNpMp, ENMpMNp, а понятия возможности и необходимости становятся излишними, поскольку каждое из последних предложений эквивалентно либо "p", либо "Np". Лукасевич считает, что причина такого положения дел заключается в невозможности сформулировать в двухзначном исчислении утверждение (II).

Следствия из утверждения (III) также не радуют Лукасевича. Используя определение универсального квантора через квантор экзистенциальный и отрицание из (III) получаем

(IV) NПpNKMpMNp.

Применяя к (IV) выводимую в Прототетике Лесьневского формулу CKfpfNpfq получаем ПpMp, т.е. все является возможным, как и ничто не является невозможным, а равно и ничто не является не необходимым. Существенная идея этого вывода в том, что функтор M является функтором в смысле Прототетики Лесьневского, т.е. экстенсиональным функтором. Взяв в качестве посылок (10) CMpp и ПpMp сразу же получаем Пp,p. А это означает, что система модальной логики, основанная на аксиомах (I)-(III) противоречива, поскольку к ее следствиям принадлежит произвольное предложение. Лукасевич заключает: "С учетом этого можно бы решить вопрос модальных предложений, основываясь на двузначном исчислении предложений, двояким образом: утверждение (I) и связанные с ним формулы первой группы [...] следует признать безусловно; в них никогда не сомневались. Из утверждений (II) и (III) можно выбрать только одно. Если мы решимся на утверждение (II) и связанные с ним формулы второй группы [...], то все модальные предложения становятся эквивалентны предложениям немодальным, следствием чего является то, что вообще не стоит вводить в логику предложения модальности; тогда нужно также отбросить весьма интуитивное понятие обоюдной возможности, как ведущее к противоречию. Если же, наоборот, решится на утверждение (III), то мы должны признать парадоксальным вывод, что все возможно, и тогда опять же нет смысла вводить модальные предложения в логику, поскольку нужно также отказаться от очевидного утверждения (II), чтобы избегнуть противоречия. Ни одно из этих решений нельзя признать удовлетворительным".(S.151)

Источником этих трудностей является интерпретация модальных функторов в двузначном исчислении предложений. В этом исчислении существует четыре одноаргументные функции: 1) f1=f0=1 (verum от p);  2) f1=0 и f0=1 (отрицание p); 3) f0=0, f1=1 (эквивалентность fp и p); 4) f1=f0=0 (falsum от p). Функтор возможности должен быть идентичен с одной из выше приведенных функций. Можно показать, что аксиомы (I)-(III) исключают некоторые случаи, например, формула CNMpNp истинна, когда Mp=fp (здесь f - falsum от p). Но главным аргументом в выборе аксиом является несогласованность (II) и (III) в том смысле, что не существует функции f такой, что Mp=fp, для которой (I) или (II) одновременно истинны. Таким образом, Лукасевичем была показана невозможность непосредственного введения модальных функторов в двузначное исчисление высказываний как с синтаксической точки зрения, так и с семантической.

Решение проблемы модальностей Лукасевич, естественно, видит в использовании трехзначной логики, а точнее - в нахождении в L₃ такого определения возможности, которое бы выполняло условия, очерченные в (I)-(III). Первая удовлетворительная дефиниция имела вид Mp=AENpПqNCpKqNq. Эта довольно сложная по свидетельству самого Лукасевича дефиниция должна быть прочитана следующим образом: "возможно, что p значит то, что "или предложение p и не-p равнозначны, или не существует такой пары противоречивых предложений, которые бы следовали из предложения p". В более общем значении понятие возможности в L₃ предложил в 1921 г. Тарский: Mp=CNpp. Дефиниенс этого определения ложен тогда и только тогда, когда p=1/2. Из этого определения и таблиц для C и N получаем равенства: M0=0, M1/2=1, M1=1. Согласно этим равенствам, если предложение p ложно, то ложно также и предложение Mp, но Mp истинно, когда p истинно или p принимает третье значение. Этот результат Лукасевич посчитал наиболее согласованным с интуицией. Определение необходимости имеет вид Lp=NCpNp в соответствии с общепринятой схемой Lp=NMNp. Заканчивая свое первое систематическое изложение модальной логики в духе логики многозначной Лукасевич полностью принимает изложенные выше определения возможности и необходимости: " Решительно не высказываясь об интуитивном смысле приведенной выше дефиниции, мы должны однако признать, что эта дефиниция удовлетворяет всем условиям, определенным в утверждениях (I)-(III), и в частности, как это доказал г.Тарский, что это единственная возможная в трехзначной системе дефиниция, выполняющая эти условия". (Лукасевич [1930], S.156)

Поскольку позже Лукасевич вернулся к проблематике модальной логики, то естественно считать, что первое ее изложение не удовлетворяло его. Новое изложение [1953] модальной логики Лукасевич начинает с изложения условий, которым по его мнению должна удовлетворять такая логика:

(1) утверждается импликация CpMp;

(2) отбрасывается импликация CMpp;

(3) отбрасывается предложение Mp;

(4) утверждается импликация CLpp;

(5) отбрасывается импликация CpLp;

(6) отбрасывается предложение NLp;

(7) утверждается эквивалентность EMpNLNp;

(8) утверждается эквивалентность ELpNMNp.

Понятия "утверждения" и "отбрасывания" принадлежат системе и обозначаются соответственно "½¾ " и "¾½ ". Первое условие соответствует принципу Ab esse ad posse valet consequentia. Второе условие соответствует высказыванию A posse ad esse non valet consequentia. В третьем условии говорится, что не все выражения, начинающиеся с M утверждаются, поскольку в противном случае Mp было бы равносильно функции "verum от p", которая не является модальной функцией. Четвертое условие соответствует принципу Ab oportere ad esse valet consequentia. Пятое условие соответствует высказыванию Ab esse ad oportere non valet consequentia. В шестом условии говорится, что не все выражения, начинающиеся с NL являются утверждениями, поскольку в противном случае Lp было бы равносильно функции "falsum от p", которая не является функцией модальности. Последние два условия представляют очевидные связи между возможностью и необходимостью.

Лукасевич предлагает для "основной модальной логики" следующую совокупность формул в качестве аксиом: (A1) ½¾ CpMp, (A2) ¾½ CMpp, (A3) ¾½ Mp, (A4) ½¾ EMpMNNp с правилами замены по определению (Lx=NMNx), подстановки в утвержденное выражение, подстановки в отбрасываемое выражение (если а отбрасывается и а есть подстановка b, то b должно быть отброшено), отделения для утвержденных выражений и отделения для отбрасываемых выражений (если Cxy утверждено, а y - отброшено, то x также отброшено). С использованием знака необходимости (A1)-(A4) преобразуются в: (A5) ½¾ CLpp, (A6) ¾½ CpLp, (A7) ¾½ NLp, (A8) ½¾ ELpLNNp. Особенно важными по мнению Лукасевича являются аксиомы (A4) и (A8). Поскольку они весьма похожи, то возникает мысль, что они имеют в своем основании некий общий принцип, из которого их можно вывести. А это значит, что "основная модальная логика" не полна. Это допущение подтверждается тем фактом, что формулы MKpqMp, CMKpqMq (если возможна конъюнкция, то возможен каждый из ее членов), а также CLKpqLp, CLKpqLq (если необходима конъюнкция, то необходим каждый из ее членов) независимы от "основной модальной логики". Не выводимы из (A1)-(A4) (либо же из (A5)-(A8)) следующие законы, известные уже Аристотелю: (a) CCpqCMpMq, (b) CCpqCLpLq, (c) CLCpqCMpMq, (d) CLCpqCLpLq. Можно показать, что из (a) следует (c), а из (b) - (d). Поэтому следовало расширить "основную модальную логику", присоединяя к ее аксиомам формулы (a)-(d). Формулы (a) и (c) можно считать частными случаями закона экстенсиональности CEpqCfpfq ("f" означает переменный функтор). Присоединяя (a) к (A1)-(A3) можно доказать (A4); аналогично присоединяя (c) к (A5)-(A7) можно доказать (A8). Однако обе конструкции Лукасевич считает недостаточно общими. Окончательная формулировка модальной системы основывается на упоминавшемся выше результате ученика Лукасевича - Мередита, утверждавшего, что L₂ и закон экстенсиональности следуют из формулы CfpCfNpfq. Окончательно аксиоматика модальной логики у Лукасевича принимает следующий вид: ½¾ CfpCfNpfq, ½¾ CpMq, ¾½ CMpp, ¾½ Mp. L-система содержит исчисление высказываний L₂, но не является двузначной. Лукасевич показал, что адекватной матрицей для L-системы является следующая четырехзначная матрица (1 является выделенным значением):

СС	11	22	33	44	Т N	MM
11	11	32	33	44	44	11
22	11	11	33	33	33	22
33	11	12	11	22	22	33
44	11	11	11	11	11	33

Из того факта, что существуют две опосредующие истину и ложь оценки (2 и 3) не следует делать вывод, что в системе модальной логики Лукасевича существуют два понятия возможности. Тем не менее в L-системе имеют место т.н. возможности-близнецы M и M₁. Они неразличимы, когда выступают отдельно, но разнятся, когда входят в одну формулу, например, формулы MMp и M₁M₁p эквивалентны, а формулы M₁Mp и MM₁p неэквивалентны. Этот факт в системе модальной логики Лукасевича не имеет интуитивной интерпретации. Четырехзначная матрица вообще изменила взгляд Лукасевича на значение многозначных логик: если раньше он считал, что выбор следует делать между трехзначной логикой или бесконечнозначной, то теперь он признал четырехзначную систему адекватной для выражения понятия возможности.

Некоторые неясные вопросы Лукасевич пытается выяснить путем сравнения с другими модальными системами, в частности, с системой фон Вригта, а не более известными системами Льюиса, поскольку "они основываются на т.н. "строгой импликации", которая более сильна, нежели "материальная импликация", используемая мной" - заключает Лукасевич (S.293). Он подвергает сомнению т.н. правило необходимости: если x является формулой системы, то L_x - также формула. Лукасевич считает, что предложение является непосредственно ложным или истинным и не видит причины, по которой тавтология должна быть "более истинной", чем "обычное" истинное предложение, а контрадикторное предложение "более ложно", чем "обычная" ложь. В этой позиции чувствуется влияние Твардовского, подкрепленное взглядами Лесьневского. Лукасевич спрашивает: "Почему мы должны вводить необходимость и невозможность в логику, если не существуют истинные аподиктические предложения? На этот упрек я отвечаю, что прежде всего мы интересуемся проблематическими предложениями вида Mx и MNx, которые могут быть истинны и используемы, хотя их аргументы и отбрасываются, а вводя проблематические предложения мы не можем обойти их отрицания, т.е. аподиктических предложений ибо предложения, обоих видов неразрывно между собой связаны".(S.295) Важной для понимания Лукасевичем понятия возможности является формула CKMpMqMKpq, не имеющая места в системе Льюиса. Лукасевич рассматривает следующий пример: "Пусть n будет целым положительным числом. Я утверждаю, что следующая импликация истинна для всех значений n: "Если возможно, что n четно, и возможно, что n нечетно, то возможно, что n четно и n нечетно". Если n=4, то истинно, что n может быть четно, но не может быть истинной, что n может не быть четным; если n есть 5, то истинно, что n может быть нечетным, но не является истинной то, что n может быть четным. Обе посылки никогда не являются одновременно истинными и пример не может быть опровергнут".(S.295) Эти рассуждения показывают, что Лукасевич понимал возможность экстенсионально, тогда как в системах Льюиса функторы L и M интенсиональны.

В варшавской логической школе исследовались также системы Льюиса. Вайсберг [1933] построил семантику для системы S5 и доказал полноту этой системы, и это было первое доказательство полноты для систем льюисовского типа. Собоцинский [1953] доказал эквивалентность модальной системы Фейса и системы M фон Вригта, а также модификации M` и M`` этой последней с системами S4 и S5; тем самым Собоцинский показал, что M, S4 и S5 являются разными системами модальной логики. Вместе с тем Собоцинский доказал, что в системе Фейса, названной T, существует бесконечно много модальностей.

 § 3. Интуиционисткая логика. Дискуссионная логика Ст.Яськовского.[36]

Первым польским логиком, занявшимся интуиционистской логикой был Яськовский [1934]. Он представил интуиционистское исчисление, аксиоматизированное Колмогоровым, в виде натурального вывода, а также заметил, что одна из аксиом А.Гейтинга независима от аксиом Колмогорова. В варшавской школе было разработано несколько аксиоматик, эквивалентных аксиомам Гейтинга. Вот некоторые из них, приводимые в книге Я.Воленского "Львовско-варшавская философская школа" [1985]:

Яськовский [1934]: CCpCqrCCpqCpr, CpCqp, CpCqKpq, CKpqp, CKpqq, CKCprCqrCApqr, CpApq, CqApq, CNpCpq, CCpNpNp;

Вайсберг [1937]: CpCqp, CCpCqrCCpqCpr, CKpqp, CKpqq, CCpqCCprCpKqr, CpApq, CpAqp, CCprCCqrCApqr, CEpqCpq, CEpqCqp, CNpCpq, CCpNpNp ;

Тарский [1938]: CxCyx, CCxCyzCCxzCyz, CxAxy, CyAxy, CCxzCCyzCAxyz, CKxyz, CKxyy, CCzxCCxyCzKxy, CNxCxy, CCNxxx, CCxNxNx ;

Лукасевич [1941]: CpCqp, CCpCpqCpq, CCpqCCqrCpr, CKpqp, CKpqq, CCpqCCprCpKqr, CpApq, CqApq, CCprCCqrCApqr, CCpNqCqNp, CNpCpq .

Вайсберг [1938] доказал т.н. утверждение о сепарации. Достаточно заметить, что аксиоматику Вайсберга (как и прочие) можно разделить на группы: две первые аксиомы содержат только знак импликации, следующие три - импликации и конъюнкции, шестая, седьмая и восьмая - импликации и дизъюнкции, девятая, десятая и одиннадцатая - импликации и эквивалентности, а последние две - импликации и отрицания. В утверждении о сепарации говорится, что каждое следствие, полученное из интуиционистского исчисления высказываний, выводится из тех аксиом, которые кроме импликации содержат исключительно функторы, входящие в данное следствие.

Тарский [1938] привел топологическую интерпретацию интуиционистской логики, а также показал [1934],[1935], что классическое исчисление высказываний является единственным непротиворечивым и полным расширением интуиционистского исчисления предложений. С последним утверждением связаны результаты Лукасевича [1941],[1952] о соотношении классического и интуиционистского исчисления высказываний. В [1941] Лукасевич пишет, что классическое исчисление сильнее интуиционистского, поскольку второе можно получить из первого путем вычеркивания одной аксиомы. Но в [1952] Лукасевич доказывает утверждение, что интуиционистское исчисление предложений содержит классическое исчисление высказываний как свою собственную часть. Он пишет: "[...] в 1938 г. я выразил взгляд, что интуиционистское исчисление предложений является только частью классического исчисления высказываний и поэтому [оно] существенно слабее, чем последнее. Сегодня я вижу, что все совершенно наоборот. Интуиционистское исчисление богаче, а значит сильнее, чем классическое. Все применения классического исчисления высказываний в математике используются также и в интуиционистском исчислении, но кроме того, в интуиционистском исчислении можно рассматривать много тонких проблем, которые не удается сформулировать в классической системе. Мне кажется, что среди известных до сих пор многозначных систем логики интуиционистское исчисление является наиболее интуитивным и элегантным" ([1952], S.267).

Сегодня известно, что классическое исчисление высказываний не может быть погружено в интуиционистское, а поэтому результат Лукасевича, учитывая также упомянутое утверждение Тарского о соотношении этих исчислений может, показаться парадоксом. Воленский [1985] дает следующее интересное объяснение сложившемуся положению: "Этот парадокс тотчас выясняется, если мы учтем, что Лукасевич пользуется не "обычным" интуиционистским исчислением предложений, но интуиционистским исчислением предложений с переменными функторами. Но и при этом предупреждении результат Лукасевича интересен с философской точки зрения, поскольку ставит вопрос: Какая система исчисления высказываний адекватно "представляет" классическую логику? Кажется, таким представлением является классическое исчисление высказываний с переменными функторами или же прототетика Лесьневского, т.е. такая система, в которой удается формализовать принцип двузначности. В свете этого комментария взгляд Лукасевича, что "все применения классического исчисления высказываний в математике используются также и в интуиционистским исчислении", кажется, все еще дискуссионным". (S.130)

Формулирование дискуссионной логики Яськовского [1948] лежит в русле той же традиции, что и первая система трехзначной логики Лукасевича, т.е. инспирирована вопросами обоснования принципа противоречия у Аристотеля, причем Яськовский продолжает исторические параллели упоминания гегелевско-марксистское понимание противоречия. Но не только исторические, параллели лежали в основе исследования Яськовского. Он приводит два мотива по существу, которые побуждают его рассматривать противоречивые системы. Первым из них является появление противоречивых утверждений вследствие неполноты выражений естественного языка, вторым - появление в эмпирических науках противоречивых гипотез, обе из которых используются при объяснении изучаемых явлений. Анализируя сложившееся положение дел Яськовский приходит к выводу, что в теории познания необходима логическая система, в которой используются противоречивые суждения. Для четкого изложения своих интуитивных взглядов Яськовский прибегает к понятию переполнения дедуктивной системы. Система S переполнена тогда и только тогда, когда произвольное правильно построенное предложение системы S выводимо из нее. Двухзначное исчисление высказываний было бы системой переполненной, если в качестве доказуемых формул содержало бы предложение x и его отрицание Nx. Однако обычное понятие противоречия и понятие переполнения взаимно не перекрываются; Яськовский же понимает противоречивость в дедуктивной системе как ее переполнение. Свою цель он видит в построении исчисления высказываний, которое: а) содержит выражения вида x и Nx без того, чтобы система была переполненной; б) было бы достаточно богато, чтобы формализовать действительно совершаемые рассуждения; в) быть интуитивно обоснованным, причем о последнем пункте Яськовский говорит, что дать ему объективную оценку трудно.

 Первым шагом в построении дискуссионной логики оказалось построение модального исчисления высказываний M2. Его можно определить как транскрипцию системы S5 Льюиса в исчисление предикатов; в этой транскрипции используется хорошо известный факт формального подобия кванторов и модальностей. Пусть x - формула, построенная при помощи пропозициональных переменных и функторов (всех или некоторых) C, A, K, N, E, L. Если заменить пропозициональные переменные одноаргументными предикатами, а L - знаком универсального квантора, то получится некоторая формула одноместного исчисления предикатов. Известно, что это исчисление разрешимо, а следовательно разрешимо и M2. В M2 можно ввести функтор возможности посредством определения Mp = NLNp.

 Предположим, что высказываемые участниками дискуссии тезисы соединены в одну систему. Может оказаться так, что эта система содержит взаимно несогласные мнения, возникшие, например, оттого, что ее содержание не связано по смыслу , хотя и необязательно. В связи с изложенным должно измениться понятие утверждения формулы в системе. Дискуссионные утверждения всегда содержат некоторые предостережения, например, "с учетом высказанного в дискуссии взгляда". Эквивалентом дискуссионного утверждения для Яськовского является функтор возможности.

Теперь легко показать, что дискуссионная система не может основываться на базе двухзначной логики. В частности из MCpq и Mp не следует Mq; правило отделения не применяется к дискуссионному утверждению. Этот факт объясняется тем, что в M2 не имеет места формула CMCpqCMpMq. Чтобы можно было применять правило отделения Яськовский вводит дискуссионную импликацию C_d и предлагает для нее в M2 дефиницию C_dpq = CMpq. Теперь позволительно использовать правило отделения, поскольку в M2 имеется формула CMCMpqCMpMq. В свою очередь вводится дискуссионная эквивалентность E_d, определяемая следующим образом: E_d = KCMpqCMqMp. Полученная система D2 может трактоваться как интерпретация системы M2, т.е. D2 представляет собой совокупность правильно построенных формул из пропозициональных переменных и функторов C_d, E_d, A, K, N, причем стоящий вначале выражения символ M свидетельствует об утверждении формулы системы M2.

Яськовский доказывает общее утверждение, говорящее, что каждая формула двузначного исчисления высказываний, не содержащая других функторов кроме C, E, A становится формулой D2, если C заменить C_d, а E - на E_d. Так формулами D2 являются выражения E_dE_dpqE_dqp и C_dC_dpqC_dC_dqp. Следующее утверждение говорит, что если X - формула двузначного исчисления высказываний, не содержащая других функторов кроме A, K, N, то X, а также C_dNXq являются формулами в D2; формулами являются выражения NKpNq (закон противоречия) и C_dKpNpq (конъюнктивный закон переполнения). Этот последний закон особенно тесно связан с идеей дискуссионной логики, ибо он утверждает, что дискуссия является переполненной, если некоторое мнение вступает в конфликт само с собой, а не тогда, когда два разных мнения находятся не в согласии друг с другом.

§ 4. Философия предложения: подводя итоги.

В предыдущих параграфах раздела, посвященных Лукасевичу, дана краткая характеристика истоков его продвижения к логике, а также отмечены важнейшие результаты и его влияние в этой области дедуктивного знания. Несомненной заслугой Лукасевича считается создание им многозначных логик.[37] И все же следует задаться вопросом: что послужило причиной разложения оценки "истина"? С учетом вышеизложенного, в частности, в связи с экстенсиональной интерпретацией функторов модальности, говорить о какой-то расчлененности предметов, даже таких абстрактных как истина или необходимая причина не приходится. Наверное, однозначного ответа на поставленный вопрос не существует. Однако некоторые соображения в этой связи, как кажется, должны быть высказаны.

Прежде чем приступить к поиску ответа на вопрос о причине деструкции истинностного значения в качестве камертона, создающего установку на анализ этой причины, примем во внимание некоторые соображения, касающиеся творчества Лесьневского. Если руководствоваться дихотомией философии языка, то Лукасевич и Лесьневский стоят в оппозиции друг к другу. Эту оппозицию удается проследить и в их творчестве. Можно было бы предположить, что для номиналиста Лесьневского, целью которого было имя существующего предмета, а средством достижения - связка "есть", такой целью окажется истинностное значение как предельное имя, тем более, что модус использования имени субъекта суждения совпадал с модусом истинностного значения как имени предложения. Однако так не случилось вследствие необыкновенно сильной установки Лесьневского на экстенсиональность. Платой за дерзость именовать предметы для Лесьневского была бесконечность процесса переименования.

С Лукасевичем дело обстоит иначе хотя бы потому, что исходным пунктом рассуждений для него был метафизический процесс, представляемый, например, отношением причинности; процесс дедукции стал и его целью. Мог ли Лукасевич, изгнавший из своей метафизики деятельностную субстанцию (предмет в случае суждения) считать ее результатом? Конечно нет. Результатом процесса, в частности, дедукции для Лукасевича оказалось истинностное значение, которое все же implicite рассматривалось им как процесс. Обобщенно говоря, поиск первых причин этого процесса привел Лукасевича к расчленению истинностного значения на части в полном согласии с той задачей, которую он поставил вначале своего творчества и которую характеризовал следующим образом: "Исследование свойств и законов тех целостностей, которые могут быть образованы предметами любого вида не принадлежит никакой частной науке, но является задачей отдельной теории целостности, являющейся частью метафизики". ([1907],S.54) Поэтому Лукасевич, поставивший процесс во главу угла, был обречен и результат, каковым оказалось истинностное значение, трактовать также. Общим в позициях Лукасевича и Лесьневского была экстенсиональность, сначала суждения, а потом и пропозиции. Причем в случае с Лукасевичем она подкреплялась устойчивой антипсихологической позицией, занятой в самом начале творчества. Уже в "Анализе и конструкции понятия причины" [1907] он пишет: "Логическая ошибка, которую обычно совершают философы состоит в том, что они не отличают предмет представлений от предмета означенного . Представленный предмет является и здесь чем-то, что появляется во внутреннем опыте, неким имманентным предметом, которым занимается психология; однако означенный предмет в этом случае является чем-то абстрактным и трансцендентным.[...] Кто не видит этой разницы, [тот] смешивает оба предмета и считает, что понятие существует во внутреннем опыте как некий духовный образ. Так возникает теория, которую согласно средневековой терминологии можно назвать концептуализмом, и которая также ошибочна, как номинализм, согласно которому общие понятия суть только слова". (S.11) Состояние же философии в начале XX ст. Лукасевич оценивает так: "Логика должна была уступить психологии познания; метафизику, ту давнюю, добрую метафизику в значении Аристотеля и схоластов, т.е. науку о том, что есть, поскольку оно есть [...] отодвинула теория познания и различного типа "критики".(S.11) Лукасевич не считает предмет необходимым, но полагает возможным обнаружить предмет познания посредством необходимых связей, отношений, для чего "нужно подробно проанализировать как понятие необходимости, так и свойства этого необходимого отношения".(S.26) Он не указывает, где размещен предмет его познания, но таковой, по всей видимости, опосредованно предполагает обнаружить в сфере метафизической, "поскольку необходимых связей в природе мы не наблюдаем".(S.26) Не предмет необходим, но необходимо существование предмета, которое Лукасевич рассматривает как отношение и процесс: "Итак, необходимым, как и ненеобходимым не может быть ни один предмет сам по себе; [...] не Бог необходим, но только Его существование".(S.49) О том, что формы существования (прежде всего необходимого) и формы суждения (прежде всего экзистенциального) Лукасевич считает аналогичными, об этом было сказано ранее. Подобие процессов существования и суждения подвинуло Лукасевича к тому, что т.н. конституционные свойства исследуемых им процессов также подобны. Эти свойства разделяются им на два класса: относительные свойства и безотносительные, причем первые относятся к процессам, а вторые - к результатам. Например, понятие причины является результатом, "реальным предметом", а свойства этого предмета - свойствами безотносительными. Аналогично и суждение будет предметом реальным и как предмет оно обладает безотносительным свойством оценочности, но как процесс - суждение относительно, т.е. ложно или истинно. Относительные свойства не интересуют Лукасевича, не они свидетельствуют о предмете метафизики. Его внимание привлекают "необходимые связи среди предметов, которыми занимается каждая наука, однако ни одна из них не исследует свойства самих необходимых отношений, которыми связаны эти предметы. Это задача науки о предметах, т.е. метафизики."(S.55)

Таким образом предметом исследований для Лукасевича является прежде всего отношение, процесс, в частности, среди "различных целостностей особенного внимания заслуживают регулярные целостности; простейшей их формой является последовательность".(S.54) Так в процессе суждения он выделяет "объективные корреляты убеждений, т.е. "объективы"", которые "изучает логика не в виду их частного содержания, но с точки зрения их формы, [...] отыскивает законы связей между истинностью и ложностью этих форм". ([1907],S.64) Отдельные формы означаются символами. Можно предположить, что среди этих символов находятся истинностные оценки, подпадающие у Лукасевича под рубрику "коррелятов суждения". Как кажется, другого объяснения природы истинностных оценок у Лукасевича нет. Его подход к истинностным оценкам метафизический, если не сказать сильнее - эмпирический. После неудачной работы о правдоподобии, обсуждавшейся выше, все аргументы Лукасевича в пользу введения третьей истинностной оценки сводятся к экстралингвистическому ее обоснованию. Говоря о принципе двузначности он пишет, что этот принцип для него неочевиден, поскольку неочевиден исход будущих случайных событий. В сущности значение оценки, отличной от истины или лжи, зависит от хода экстралингвистического процесса. Но этот же эффект можно было наблюдать и при анализе предложений правдоподобия. Впрочем, Лукасевич и не скрывает своего незнания природы истинностных оценок, ибо она для него процесс и интересовать его могут только свойства этого процесса. В статье "О детерминизме"[1922] он пишет: "Чем является эта третья логическая оценка? У меня нет для нее соответствующего названия".(S.125) Интерпретируя ее как "возможность" Лукасевич только подчеркивает эмпирический характер третьей истинностной оценки в виде возможности появления будущего события.

О том, что экстралингвистическая (эмпирическая) интерпретация третьей истинностной оценки была выбрана неудачно свидетельствуют трудности с интерпретацией оценок тогда, когда число их увеличивается. В этой ситуации просто необходимо задаться вопросом об интерпретации истинностных оценок: соответствуют ли их значениям какие-либо экстралингвистические предметы, коррелятами которых являются оценки, или же они суть результаты интралингвистических процессов? И в первом, и во втором случае оценки могут быть метафизическими предметами. В этой ситуации совершенно очевидной становится позиция Лукасевича и в отношении логических функций, значениями и аргументами которых являются эти истинностные оценки: "Понятия пропозициональной переменной, импликации и отрицания не могут быть подробнее объяснены; их следует считать первичными понятиями методологии исчисления предложений". ([1930],S.130) Для Лукасевича логика - это инструмент, которым как сетью можно вылавливать "жемчуга научного синтеза". Именно в силу этого взгляда на логику он придавал большое значение т.н. "обобщающей дедукции", когда посылка в выводе является с синтаксической точки зрения частным случаем заключения. Этот свой взгляд он распространил и на традиционную логику: "В учебниках логики мы часто встречаемся со взглядом, что дедукция - это вывод от общего к частному. Этот взгляд ошибочен уже в области традиционной логики". И далее: "Одновременно с этой ошибочной характеристикой дедукции низлагается по определению и взгляд, будто бы дедукция не расширяет нашего знания". ([1931],S.173) Примеров расширения "нашего знания" с точки зрения семантики Лукасевич не приводит, ибо такие примеры предполагали бы интерпретацию в конечном счете предложений логического исчисления, а подобное действие связано с номинализмом. В [1936] Лукасевич еще связывает определенные надежды с номинализмом, ибо пишет, что "современная логика одета в номиналистические одежды", но уже в [1937] его отношение меняется: "Признаюсь совершенно искренне, что если бы еще недавно мне кто-нибудь задал вопрос, признаю ли я как логик номинализм, то ответил бы утвердительно, без колебаний, поскольку не задумывался глубже над самой доктриной номинализма, но обращал внимание только на логическую практику".(S.212) Правда, номинализм Лукасевич понимал весьма радикально, считая, что "логистика заняла бы номиналистическую позицию, если бы имена и предложения трактовала исключительно как записи определенной формы, не беспокоясь тем, означают ли что-нибудь эти записи и что они значат".(S.213) Дело даже не в том, что совокупность написанных знаков конечна: "против номинализма, продуманного мною до конца восстает вся моя интуиция".(S.213) Сравнивая логику с шахматами, в которых фигуры по мнению Лукасевича ничего не значат, а логические знаки имеют смысл, он свою задачу видит в нахождении этого смысла "в мыслях и значениях, выражаемых знаками, хотя бы мы и не знали, что это за значения, но никак в самих знаках".(S.213) Решение Лукасевича - это компромисс, выраженный оборотом "хотя бы мы и не знали, что это за значения". Под компромисс подводится философский фундамент: "О изложенном выше я говорю как философ, не как логик. Логистика не может решить этот вопрос, ибо не является философией. Тем более ее нельзя обвинять в номинализме".(S.214) В конечном счете компромисс распространяется и на философию: "Я не отрицаю метафизики, не осуждаю философии, ни к одному философскому направлению не отношусь с предубеждением, только не признаю неряшливой работы мысли".(S.214) А поскольку дело обстоит таким образом, то не следует искать источник помыслов создания многозначных логик в философии, понимая ее как процесс или течение человеческой мысли, движущейся определенным руслом. И тогда теряется цель продвижения, философия становится теорией, что развивается от результата к результату эмпирическим путем, теряя свой метод; логика же при этом рассматривается как инструмент. Свидетельства Лукасевича на сей счет не оставляют сомнений: "Как создатель многозначных систем логики предложений я прежде всего утверждаю, что исторически эти системы не выросли на почве конвенционализма или релятивизма, но возникли на фоне логических исследований, касающихся предложений модальностей и связанных с ними понятий возможности и необходимости".(S.216-217) При таком подходе философия сужается до метафизики и приобретает исключительно научный характер. Лукасевич продолжает: "Я неоднократно задавался вопросом, утверждать ли, что существуют предложения о фактах, имеющие третье логическое значение. Логический вопрос здесь преобразуется в онтологическую проблему, касающуюся строения мира."(S.218) Поэтому никакая интерпретация третьего истинностного значения не может помочь в объяснении строения мира.

Трудность с интерпретацией истинностных значений была замечена вскоре после создания многозначных логик. Даже в отношении принципа противоречия (не говоря уже о принципе исключенного третьего) заметна несогласованность исходных позиций Лукасевича и полученных им результатов. Он пишет: "Кто бы там не хотел что-нибудь сказать плохое о многозначных логиках, все же тот не может отрицать того, что несмотря на их существование нетронутым остался принцип исключенного противоречия. Это истина безотносительная, обязывающая все логические системы под угрозой, что в случае ее преступления вся логика и вообще все научные исследования стали бы бесцельными".(S.219) На первый взгляд складывается парадоксальная ситуация: в L₃ принцип противоречия не имеет места, но является "безотносительной истиной". Действительно, пусть предложение a имеет оценку 1/2 (a=1/2). Тогда в соответствии с таблицей отрицания в L₃ не-a = 1/2. Конъюнкция в L₃ определяется таким образом, что предложение "a и не-a"=1/2, если члены конъюнкции имеют оценки 1/2. Наконец, предложение "не-(a и не-a)"=1/2 и оно не является тавтологией L₃. Однако достаточно вспомнить, что Лукасевич формулировал принцип противоречия (позже он говорил о "принципе исключенного противоречия") следующим образом: два противоречащих предложения не могут быть одновременно истинными. Это последнее утверждение вовсе не противоречит тому факту, что для a=1/2 закон противоречия не имеет места, поскольку тот факт, что a=1/2 и не-a=1/2 не означает, что a=1 и не-a=1. Поэтому для многозначных логик можно сформулировать обобщенный принцип противоречия: два отрицающих друг друга предложения не могут иметь выделенного значения и, как легко видеть, случай a=1/2 и не-a=1/2 не вступает в конфликт с обобщенным принципом противоречия. Этот случай свидетельствует только о том, что два противоречащих друг другу предложения могут обладать невыделенными значениями.

Аналогично можно сформулировать и обобщенный принцип исключенного среднего: из двух противоречащих друг другу предложений одно должно иметь выделенное значение. И этот принцип не имеет места в L₃, но можно представить себе систему с n> 2 (ревизия принципа двузначности), сохраняющую принцип исключенного среднего так же, как существуют двузначные системы, не являющиеся классическими; все зависит от определения логических функторов отрицания и дизъюнкции

Этот вывод применительно к логическому творчеству Лукасевича не является неожиданным: тот, кто выбрал процесс точкой приложения своих усилий должен сделать его и предметом, т.е. результатом изучения. Тот факт, что уровень процессов оказался синтаксическим свидетельствует лишь о том, что язык для Лукасевича начинал выполнять роль эмпирии. Вот как он описывал тот образ, что возникал у него в связи с изучением логического синтаксиса языка: "Сколько бы я не занимался даже мельчайшими логическими проблемами, ища, например, кратчайшую аксиому импликативного исчисления, столько же и чувствую, что нахожусь рядом с какой-то мощной, неслыханно сплоченной и неизмеримо крепкой конструкцией. Эта конструкция действует на меня как некоторый конкретный осязаемый предмет, сделанный из самого твердого материала, во сто крат тверже, чем бетон и сталь. Ничего я в ней изменить не могу, ничего произвольно не создаю, но напряженным трудом открываю в ней все новые и новые подробности, достигая истин непоколебимых и вечных. Где и чем является эта идеальная конструкция? Верующий философ сказал бы, что она в Боге и является Его мыслью."(S.219)

В завершение представленного здесь успеха в изучении синтаксиса и неудачи в семантике следует очертить отношение Лукасевича, если не к прагматике, как части семиотики, то к прагматизму. Свидетельств отрицательного отношения Лукасевича к прагматизму в связи с вопросом об истинностном значении достаточно. Он прямо пишет: "Не признаю прагматизм как теорию истины и считаю, что никто, будучи рассудительным, не признает этой доктрины. Не думаю также и о том, чтобы прагматически проверять истинность логических систем. Логические системы не требуют такой проверки. Я хорошо знаю, что все логические системы, которые мы создаем, при тех предпосылках, при которых они создаются, истинны по необходимости".(S.218) Однако в подходе к номинализму прагматизм редуцировался к прагматике. Лукасевич писал, что математическая логика имеет номиналистическое одеяние, т.к. трактует предложения и имена как записи определенной формы, а не рассматривает их как суждения или понятия. Номинализм вызывал в нем сомнения, как кажется, практического характера, поскольку номиналистически записи должны пониматься как конечное множество инскрипций, ибо человек может создать только конечное их количество. Между тем логические и математические системы (в смысле Тарского) составлены из бесконечного числа формул. Защита номинализма, состоящая в ограничении множества формул где-то и когда-то записанных делает невозможным использование методов метаматематики. Поэтому Лукасевич считает, что логики и математики используют лишь номиналистическую терминологию, а в сущности не являются номиналистами: исследуемая логиками реальность лежит вне сферы записей. А поскольку Лукасевич не занимал какой-либо выразительной философской позиции, то опять же реальность, с которой он имел дело, сводилась не к процессам этой реальности, т.е. экстралингвистическим, а к процессам интралингвистическим; в них он видел и результат этих процессов, т.е. предмет исследования, который должен быть назван. Таким образом Лукасевичу не удалось избежать номинации, но номинации интралингвистической, осуществляемой логическими функторами, т.е. просто говоря, номинации результата интралингвистического процесса, коим была правильно построенная формула. Философ, поставивший во главу угла процесс, отношение, а также поиск этих простых и необходимых отношений был обречен, будучи и логиком, именовать результаты этих процессов. Подобно тому как Лесьневский был обречен на бесконечный процесс номинации, видя перед собой предмет и его имя, так и Лукасевич, поставивший целью процесс, свел его в конечном счете к результату и имени, сделав это однако на синтаксическом уровне, ибо на этом уровне процесс и результат эквивалентны. Выражением результата стала бесскобочная нотация. Там же, где акцент делался на процессе, например, вывода, там тот же естественный вывод Яськовского не получил распространения, хотя и был открыт значительно раньше генценовского. Эта первая неудача никого не насторожила в варшавской логической школе и тому были свои причины. Прежде чем их упомянуть, вспомним, что генценовская форма записи правил содержит как изображение процесса вывода, с участвующими в нем формулами, так и результат этого процесса. Резюмируя можно сказать, что префиксная форма записи формул не всегда пригодна для изображения процесса, даже интралингвистического, т.е. на синтаксическом уровне. Таким образом, Лукасевичем процесс, в частности, семиотический процесс записи формул посредством функторов, был фактически исключен из логической практики. Естественно, немедленно последовала реакция и процесс был восстановлен: операция Cn(X) присоединения следствий явилась тем компенсаторным механизмом, что вознес логику на более высокий уровень метатеории. Попутно следует отметить ту интересную деталь, что Лукасевич, на семинарах которого были получены фактически все логические результаты, сам практически не пользовался понятием метатеории вплоть до последних публикаций.

Другой особенностью кодификационной системы Лукасевича является трактовка модальностей как функторов, понимаемых, впрочем, экстенсионально. Эта особенность неудивительна, если учесть, что в польской нотации синтаксис логических функторов и операторов модальностей одинаков. Но, очевидно, что семантика модальностей и логических знаков различна: первые соотносятся с положением дел в реальности непосредственно и у Лукасевича выражают вследствие своей экстенсиональной трактовки положение вещей, что можно было бы обозначить терминами "Sachverhalt" или "объектив", которыми он пользовался в раннем периоде творчества, вторые же соотносятся с реальностью опосредованно, через истинностные оценки. Если логический знак, с учетом его роли не только в тавтологиях, может быть назван маркером целостности, то оператор модальности - маркером анализа, разлагающим оценку "истина".

§ 5. Исторические исследования логики Я.Лукасевичем.

 Лучшим подтверждением изложенного выше тезиса о том, что творчество Лукасевича развивалось в парадигме философии предложения, а не имени может служить сравнение им двух подходов к логике - у Аристотеля и стоиков. Совершенно явным образом Лукасевич отдает предпочтение последнему. Прежде чем перейти к систематическому изложению исторических исследований приведем цитату, которая позволит расставить акценты в диалектике древних авторов. В работе "Из истории логики предложений"[1934] Лукасевич пишет: "Основное различие, которое имеет место между логикой стоиков и аристотелевской логикой состоит в том, что в стоической диалектике имеются условные и разделительные периоды, тогда как в аристотелевской логике имеются только категорические предложения. [...] Основное различие между этими двумя античными системами состоит в том, что в стоических силлогизмах переменные являются пропозициональными переменными, а в аристотелевских - именными".(S.180) Важно подчеркнуть, что среди "основных различий" Лукасевич не видит связки <есть>, т.е. его совершенно не интересует, каким образом строится из имен категорическое предложение: он принимает его как данное, отмечая лишь различие внешнее в виде различия синтаксических категорий. Эта аберрация зрения представляет собой разительный контраст с позицией Лесьневского, для которого связка <есть> была основным средством для получения тех же предложений.

 Изучая логику стоиков Лукасевич [1927],[1934] показал, что их логика была логикой предложений, а не логикой имен. Поэтому логика стоиков - это система правил вывода, а не совокупность формул. Таким образом, между этими логиками имеется двойное различие: аристотелевская логика является логикой имен и системой предложений, а логика стоиков - логикой предложений и системой правил вывода. Однако, как показал Лукасевич, стоики знали метод преобразования правил в формулы; так они говорили, что силлогизм, состоящий из посылок x и y и заключения z называется правильным, если истинной является импликация CKxyz. Лукасевич также показал, что т.н. недоказуемые силлогизмы стоиков, например, правило отделения, выполняют роль аксиоматических правил. Выяснены Лукасевичем также и некоторые метатеоретические вопросы логики стоиков: эта логика была сугубо двузначной, в ней использовалось понятие истинностнозначной функции, в частности, стоикам были известны отрицание, импликация, конъюнкция и разделительная дизъюнкция. Они были знакомы со спорными вопросами, связанными с интерпретацией импликации. В силлогизмах стоики использовали материальную импликацию, определенную Филоном из Мегары, но другой мегарец - Диодор говорил, что импликация истинна тогда и только тогда, когда антецедент не может быть истинным, а консеквент - ложным. Подытоживая особенности логики стоиков Лукасевич указывает, что они вполне осознавали, что ими была создана система совершенно отличная от логики Аристотеля и более фундаментальная.

 Взгляд Лукасевича на историю логики удается уточнить в результате сравнения двух наиболее старых теорий силлогистики: условного силлогизма стоиков и категорического силлогизма Аристотеля. Большинство фактов, которые приводит Лукасевич для обоснования интерпретации логики стоиков были известны и ранее, в частности тот, что стоики некоторые правила вывода принимали как недоказуемые или же использовали смысл импликации. Лукасевич задается вопросом: почему эти факты не трактовали надлежащим образом? По его мнению ошибки предыдущих историков логики объясняются незнанием ими формальной, или математической логики, которую они и не могли знать. Таким образом, считает Лукасевич, компетентным историком логики может быть только тот, кто усвоил основные достижения современной логики. Более того, по мнению Лукасевича, математическая логика является естественным обобщением традиционной формальной логики и поэтому для понимания последней необходимо знакомство с первой.

 С этих позиций Лукасевич [1939] пробует ответить на вопрос: "[...] Какой силлогизм является первым, категорический или гипотетический". Он продолжает: "Итак категорический силлогизм является аристотелевским силлогизмом, а гипотетический - стоиков. Наш спорный вопрос тем самым касается отношения аристотелевской логики к [логике] стоиков и сводится к утверждению, какая из этих систем первая, т.е. по моему мнению, какая является первой логически".(S.187) Ответ Лукасевича категоричен: "Сегодня мы знаем, что логика предложений имеет несравненно большее значение, чем этот убогий фрагмент логики имен, который содержится в аристотелевской силлогистике. Логика предложений является фундаментом всех логических и математических систем".(S.188) Единственное достоинство, которое видит Лукасевич в системе Аристотеля - ее построение аксиоматическим методом. Несомненно, реконструкция логики стоиков Лукасевичем оказалась значительным достижением, получившим всеобщее признание, чего нельзя сказать про реконструкцию силлогистики Аристотеля, которой, как считает польский логик, он возвращает первозданную форму.

 Ревизия силлогистики Аристотеля была начата Лукасевичем в ряде статей [1934],[1939] и систематически изложена в монографии [1951a] с участием Слупецкого [1949]. Уже в [1934] он заметил, что Аристотель силлогизмы формулировал в виде импликации, а не как правила вывода. Например, модус Barbara представляет собой предложение <если каждое M есть P и каждое S есть M, то каждое S есть P>, но не является правилом для посылок <каждое M есть P>, <каждое S есть M> и заключения <каждое S есть P>. Лукасевич утверждает, что Аристотель формулировал свои силлогизмы исключительно при помощи общих терминов.

 В более поздних работах [1939],[1951a] Лукасевич видит силлогистику как аксиоматическую систему, в которой возможно применение законов исчисления высказываний. Этот взгляд послужил основанием для интерпретации логики Аристотеля как аксиоматической системы в современном ее понимании. Силлогистика надстроена над исчислением высказываний, т.е. в логике Аристотеля, считает Лукасевич, можно пользоваться всеми законами исчисления предложений. Первичными символами, называемыми также функторами, являются символы U (каждый ... есть) и I (некоторые ... есть), а аксиомами - формулы (малые литеры обозначают переменные для имен) Uaa, Iaa, CKUmbUamUab, CKUmbImaIab. Две первые аксиомы являются формализацией закона тождества, а две вторые - представляют в понимании Лукасевича силлогизмы Barbara и Datisi. Частноотрицательное и общеотрицательное суждения вводятся посредством дефиниций: Oab=NUab и Yab=NIab соответственно. Правилами вывода служат правило отделения, подстановки предложений вместо пропозициональных переменных и имен вместо переменных для имен, а также замены по определению. В так сконструированной силлогистике невозможно получить силлогизмы, отбрасываемые Аристотелем, но и невозможно показать, что эти силлогизмы неверны. Чтобы разрешить этот вопрос Лукасевич расширяет систему и вводит отбрасываемые силлогизмы - прием, введенный впервые в практике дедуктивных систем. В качестве отбрасываемых аксиом Лукасевич вводит формулы ¾½ CKUbmUamIab и ¾½ CKYbmYamIab, а все ложные силлогизмы исключаются сведением их к отбрасываемым аксиомам при помощи правил: а) можно отбросить каждое выражение, из которого путем подстановки получается отбрасываемое выражение; б) если утверждается импликация Cxy и отбрасывается ее консеквент, то можно отбросить и антецедент.

 Так сконструированная логика категорических предложений позволяет вывести все правильные силлогизмы, в ней выполняются все законы непосредственного вывода (логический квадрат, конверсия и т.д.), а также отбросить все 232 модуса силлогистики, дающие ложные заключения. Однако эта система оказалась не совсем разрешимой, ибо в ней не удается отбросить все ложные выражения, например, CKOabObaYab. Решающим шагом в направлении вопроса о разрешимости было формулирование Слупецким специального правила отбрасывания, т.н. правила Слупецкого. Пусть x и y обозначают выражения типа Yab либо Oab, а z - т.н. простое выражение, т.е. Uab, или Iab, или Oab, или Yab, или импликацию, консеквент которой является простым выражением, или конъюнкцией таких простых выражений. Тогда, если отбрасываемы импликации Cxz и Cyz, то отбрасываема также импликация CKxyz. Лукасевич [1939a] дает следующее объяснение мотивам Слупецкого: "Интуитивный смысл этого правила остается в связи с известным утверждением: ex mere negativis nihil sequitur. Никакое нагромождение противоречивых посылок не достаточно для доказательства какого-либо заключения, если это заключение не следует ни из одной из этих посылок отдельно".(S.226) Результат Слупецкого был оценен Лукасевичем как "важнейшее открытие, сделанное в области силлогистики со времен Аристотеля".(S.226)

 Реконструкция аристотелевской силлогистики Лукасевичем несомненно является выдающимся достижением формальной логики, однако в результате некоторых модификаций утрачена цель, поставленная Стагиритом. А именно, заключение силлогизма по Лукасевичу может быть истинным, но оно ничего не говорит о сути вещи, которая должна раскрываться по замыслу Аристотеля в силлогизме. Для ее высказывания необходимо расшифровать отношения Uab, Yab, Iab, Oab, выражения которых служат именами для этих отношений. Таким образом, если Лукасевич редуцирует логику имен к логике предложений, то он все таки вынужден вводить имена, но уже для отношений, сводя роль терминов к статусу переменных, т.е. лишая их семантической компоненты. Если связь посылок у Аристотеля осуществляется средним терминов, то для Лукасевича на синтаксическом уровне достаточно конъюнкции. Несмотря на то, что Лукасевич осознает роль имен в силлогистике Аристотеля, в реконструкции этой системы имя играет подчиненную роль и привлекает внимание польского логика главным образом при рассмотрении непосредственного вывода. Система Аристотеля сводится к четырем константам U, Y, I, O и пропозициональным константам "если, то", "и", "не", называемых в совокупности функторами. Если учесть, что пропозициональные константы принимаются в качестве неопределяемых понятий, то к таковым следует отнести также и функторы U, Y, I, O. Между тем аргументы этих функторов отличны от аргументов пропозициональных констант и Лукасевич прекрасно видит эту разницу, однако находясь в парадигме философии предложения он сводит путем именования отношений имена в посылках к пропозиции. Так оно и в действительности есть, ибо силлогистика оперирует реальными суждениями, которые оцениваются как ложные или истинные. Будучи логикой, силлогистика, по мнению Лукасевича, ничего не говорит о существовании. Именно поэтому Лукасевич совершенно игнорирует значение среднего термина. А ведь средний термин вследствие его тождественности в посылках - это единственный термин, из modi significandi которого (при сведении к I фиг.) можно заключить непосредственно о существовании обозначаемого предмета.[38]

Но самый "большой дефект аристотелевской логики", по мнению Лукасевича, состоит в том, что "в ней не нашлось места единичным терминам и предложениям". ([1951a], С.40) О единичных терминах в предложениях вида "то белое есть Сократ" можно сказать вслед за Аристотелем, что они бывают "случайно" истинными. Эту случайность можно объяснить тем, что Аристотель не хотел ничем ограничивать форму суждения, сознательно разделив определение и суждение (реальное ). Если бы он осознавал, что номинальное суждение как вид определения поставляет имена для суждения реального, то не отмечал бы, что единичный термин не может быть предикатом истинного предложения, так же как и наибольший термин не может быть субъектом такого предложения. Лукасевич приводит это замечание Аристотеля в своей работе и приветствует его потому, что общий термин открывает путь к переменным в силлогистике, введение которых польский логик считает величайшей заслугой древнегреческого логика. И это понятно, ведь переменная - это путь к формализации, которую Лукасевич считает предпосылкой научного изложения. Формализации же в логическом творчестве самого Лукасевича подвергается главным образом предложение.