Математическая логика. Ее еще называют
символической логикой. М. л. — это
та же самая Аристотелева силлогистическая логика, но только громоздкие
словесные выводы заменены в ней математической символикой. Этим достигается,
во-первых, краткость, во-вторых, ясность, в-третьих, точность. Приведем
пример. Известный силлогизм. Большая посылка: «Все люди смертны». Малая
посылка: «Сократ — человек». И вывод: «Следовательно, Сократ смертен».
Мы можем заменить имена «Сократ», «человек» и свойство «быть смертным»
буквами, соответственно С, х и у. Слово «все» называется квантором всеобщности
— о нем мы скажем ниже. Оно обозначается так называемой гротесковой перевернутой
буквой А: 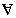
Итак, запишем символически большую посылку:
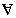 (x)(y), то есть для всех индивидов х соблюдается свойство у — все люди
смертны. Теперь запишем символически малую посылку С(х), то есть индивид
С обладает свойством х, — Сократ смертен. И вывод: С(у), то есть индивид
обладает свойством у. Сократ смертен. Теперь запишем весь силлогизм в виде
импликации (логического следования):
(x)(y), то есть для всех индивидов х соблюдается свойство у — все люди
смертны. Теперь запишем символически малую посылку С(х), то есть индивид
С обладает свойством х, — Сократ смертен. И вывод: С(у), то есть индивид
обладает свойством у. Сократ смертен. Теперь запишем весь силлогизм в виде
импликации (логического следования):
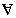 (x)(y)&;C(x)
(x)(y)&;C(x)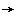 C(y)
C(y)
То есть, «если все люди смертны и Сократ человек, то Сократ смертен». Если записывать словами, то надо использовать более 60 символов (букв), а если символически, то нужно всего 12 символов, в 5 раз меньше. Если нужно решать сложную задачу, экономия становится очевидной.
Так или иначе, но только в конце ХIХ в. немецкий логик Готтлоб Фреге сформулировал символическое исчисление, и лишь в начале XХ в. Бертран Рассел и Альфред Уайтхед в трехтомном труде «Principia Mathematica» построили стройную систему М. л.
В М. л. два типа символов — переменные, которые обозначают объекты, свойства и отношения; и связи, символизирующие логические отношения между предметами и высказываниями. Для наших целей достаточно различать следующие связки:
&; — конъюнкция, соединение; читается как союз «и», во многом соответствует ему по смыслу;
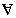 — дизъюнкция, разделение; читается как союз «или»;
— дизъюнкция, разделение; читается как союз «или»;
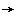 — импликация, следование; «если... то...»;
— импликация, следование; «если... то...»;
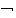 — отрицание; «неверно, что...»;
— отрицание; «неверно, что...»;
= — эквивалентность; «то же, что и...»
В основе любой логической системы лежат несколько недоказуемых очевидных аксиом, так называемых законов логики. В обычной двузначной логике, то есть в такой логике, высказывания которой имеют два значения (истина и ложь), выделяют четыре основных закона.
1. Закон тождества: р = р; то есть любое высказывание эквивалентно самому
себе. Тождество объекта самому себе — вообще исходное начало для любого
мышления. Но не во всякой логике это является законом. Например, в контексте
алетических модальностей (см. модальности![]() )
мы можем сказать: «Возможно, что дождь идет» и «Возможно, что дождь не
идет» — и это не будет противоречием. В обычной логике пропозиций предложения
«Идет дождь» и «Не идет дождь» будут противоречиями.
)
мы можем сказать: «Возможно, что дождь идет» и «Возможно, что дождь не
идет» — и это не будет противоречием. В обычной логике пропозиций предложения
«Идет дождь» и «Не идет дождь» будут противоречиями.
2. Закон двойного отрицания: р = 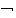
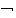 р; то есть утверждение эквивалентно
его двойному отрицанию. «Дождь идет» = «Наверно, что Дождь не идет».
р; то есть утверждение эквивалентно
его двойному отрицанию. «Дождь идет» = «Наверно, что Дождь не идет».
3. Закон исключенного третьего: p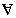
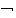 p то есть либо высказывание истинно, либо оно ложно — третьего
не дано (применимость закона исключенного третьего ограничена конечными
множества объектов; см. об этом многозначные логики).
p то есть либо высказывание истинно, либо оно ложно — третьего
не дано (применимость закона исключенного третьего ограничена конечными
множества объектов; см. об этом многозначные логики).
4. Закон противоречия: 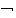 (р &
(р & 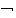 р); то есть неверно, что высказывание
может быть одновременно истинным и ложным.
р); то есть неверно, что высказывание
может быть одновременно истинным и ложным.
Следует ввести еще два понятия, одно из которых мы уже ввели в самом
начале статьи. До сих пор мы говорили о высказывании как о чем-то нерасчлененном,
но у высказывания есть субъект и предикат. Часть М.
л., занимающаяся отношениями между субъектом и предикатом высказываний,
называется теорией квантификации. Свойство или отношение, которое выражает
предикат, может быть присуще всем субъектам данного множества или только
некоторым из них. Например, высказывание «Собаки бывают черными» означает,
что некоторое количество собак из всего множества собак имеет свойство
«быть черным». Символ, на который мы заменим слово «некоторые», называется
квантором существования, или экзистенциальным квантором, и обозначается
гротесковой обращенной буквой E: 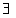
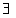 (х)(у) — некоторые собаки черные.
(х)(у) — некоторые собаки черные.
Но существуют свойства, характерные для всех собак. Например, у всех собак (разумеется, живых) есть голова. Символ, на который мы поменяем слово «все», это уже известный нам квантор всеобщности, или универсальный квантор:
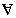 (х)(у) — все собаки по природе обладают головой.
(х)(у) — все собаки по природе обладают головой.
В заключение сформулируем основной закон квантифицированной логики:
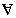 (х)(у)
(х)(у)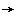
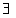 (х, у)
(х, у)
То есть если данным свойством обладают все объекты, то им обладают и некоторые объекты. Кажущаяся тривиальность законов логики оправдывается дальнейшим ходом мышления. Как писал Людвиг Витгенштейн, «Если вы знаете, что у вас есть руки, дальнейшее гарантируется».
О том, как М. л. связана с внешним
миром, см. логическая семантика![]()
![]() .
.
| Лит.: | Клини С. Математическая логика. — М., 1974.
Черч А. Введение в математическую логику. — М., 1959. |
| В.Руднев «Словарь
культуры ХХ в.» Математическая логика |