Многозначные логики. Обычная Аристотелева
логика называется двузначной, потому что ее высказывания, имеют два значения,
то есть они могут быть либо истинными, либо ложными (см. также математическая
логика![]() )
Однако мы знаем, что в реальности
)
Однако мы знаем, что в реальности![]() далеко не всегда можно определить точно истинность или ложность
высказывания, и бывают переходные случаи. Например, есть высказывания неопределенные
с точки зрения их истинности или ложности:
далеко не всегда можно определить точно истинность или ложность
высказывания, и бывают переходные случаи. Например, есть высказывания неопределенные
с точки зрения их истинности или ложности:
Коммунизм — это молодость мира.
Нынешний король Франции лыс.
Вот что пишет по этому поводу один из виднейших современных философов Георг Хенрик фон Вригт: «Возьмем, например, процесс выпадения дождя. Этот процесс продолжается некоторое время, а затем прекращается. Но предположим, что это происходит не внезапно, а постепенно. Пусть
р .............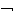 р
р
иллюстрирует, что на определенном отрезке
времени![]() вначале определенно идет дождь, потом определенно не идет дождь
(
вначале определенно идет дождь, потом определенно не идет дождь
(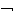 р), а между этими временными точками находится переходная область,
когда может капать небольшое количество капель — слишком мало для того,
чтобы заставить нас сказать, что идет дождь, но слишком много для того,
чтобы мы могли воздержаться от утверждения, что дождь опредленно закончился.
В этой области высказывание р ни истинно, ни ложно».
р), а между этими временными точками находится переходная область,
когда может капать небольшое количество капель — слишком мало для того,
чтобы заставить нас сказать, что идет дождь, но слишком много для того,
чтобы мы могли воздержаться от утверждения, что дождь опредленно закончился.
В этой области высказывание р ни истинно, ни ложно».
Таким образом, появляется еще третье значение высказывания: «ни истинно, ни ложно»; или «и истинно, и ложно»; или «неопределенно».
Когда соответствующие явления стали обнаруживаться в математике и физике
— например в квантовой механике при описании микромира, частица может производить
одновременно воздействия на места, в которых она сама не находится, или
как в трансперсональвой психологии![]() , когда сознание настолько расширяется, что может одновременно находиться
в разных местах, — то назревает необходимость в адекватном описании таких
аномальных, с точки зрения двузначной логики, явлений. Здесь-то и помогает
аппарат многозначной, например трехзначной, логики, которая наряду с обычными
значениями «истинно» и «ложно» оперирует значением «неопределенно», или
«неизвестно», или «ненаблюдаемо».
, когда сознание настолько расширяется, что может одновременно находиться
в разных местах, — то назревает необходимость в адекватном описании таких
аномальных, с точки зрения двузначной логики, явлений. Здесь-то и помогает
аппарат многозначной, например трехзначной, логики, которая наряду с обычными
значениями «истинно» и «ложно» оперирует значением «неопределенно», или
«неизвестно», или «ненаблюдаемо».
Мы знаем (см. математическая логика![]() ),
что в основе логического исчисления лежат несколько самоочевидных истин,
аксиом, которые мы называем законами логики. В обычной двухзначной логике
таких законов четыре: закон тождества (любое высказывание с необходимостью
равно самому себе); закон двойного отрицания (двойное отрицание высказывания
равно утверждению этого высказывания); закон исключенного третьего (высказывания
может быть либо истинным, либо ложным); закон противоречия (неверно, что
высказывание может быть одновременно истинным и ложным).
),
что в основе логического исчисления лежат несколько самоочевидных истин,
аксиом, которые мы называем законами логики. В обычной двухзначной логике
таких законов четыре: закон тождества (любое высказывание с необходимостью
равно самому себе); закон двойного отрицания (двойное отрицание высказывания
равно утверждению этого высказывания); закон исключенного третьего (высказывания
может быть либо истинным, либо ложным); закон противоречия (неверно, что
высказывание может быть одновременно истинным и ложным).
В начале ХХ в. выяснилось, что закон исключенного третьего, строго говоря,
не является законом логики, в силу того, что он действует только применительно
к конечному множеству объектов, тогда как, например, числа представляют
собой бесконечное множество. Вот что пишет об этом известный логик, а также
автор знаменитых диссидентских памфлетов А. А. Зиновьев:
«Возьмем утверждение: всякое целое число, большее единицы, есть либо простое,
либо сумма двух простых, либо сумма трех простых. Неизвестно, так это или
нет, хотя во всех рассмотренных случаях это так (а их конечное число).
Назовем исключительным числом число, которое не удовлетворяет принятому
утверждению. Существует ли такое число или нет? Мы не можем указать такое
число и не можем вывести противоречие из допущения его существования![]() . Отсюда делается вывод о неприменимости закона исключенного третьего
в таких случаях». В данном случае, также показывающем, что не все законы
двухзначной логики срабатывают, речь шла о так называемом интуиционистском
понимании логики (авторы концепции интуиционизма — Л.
Броуэр и А. Гейтинг).
. Отсюда делается вывод о неприменимости закона исключенного третьего
в таких случаях». В данном случае, также показывающем, что не все законы
двухзначной логики срабатывают, речь шла о так называемом интуиционистском
понимании логики (авторы концепции интуиционизма — Л.
Броуэр и А. Гейтинг).
Аналогичным образом, двухзначная логика плохо описывает некоторые модальные
высказывания (см. модальности![]() ).
Например, высказывания «возможно, идет дождь» и «возможно, не идет дождь»
не противоречат друг другу. Может быть, идет, а может, уже кончился. Но
их немодальные аналоги — «дождь идет» и «дождь не идет» — являются явными
противоречиями. Для подобных случаев и создавались М.
л. Их авторы — Я. Лукасевич,
Э. Пост, Д.
Бочвар, Г. Рейхенбах
стремились более адекватно, чем это делает классическая двузначная логика,
описать такие сложные процессы, как процессы в микромире, или обойти такие
технические трудности, как в примере с модальными высказываниями.
).
Например, высказывания «возможно, идет дождь» и «возможно, не идет дождь»
не противоречат друг другу. Может быть, идет, а может, уже кончился. Но
их немодальные аналоги — «дождь идет» и «дождь не идет» — являются явными
противоречиями. Для подобных случаев и создавались М.
л. Их авторы — Я. Лукасевич,
Э. Пост, Д.
Бочвар, Г. Рейхенбах
стремились более адекватно, чем это делает классическая двузначная логика,
описать такие сложные процессы, как процессы в микромире, или обойти такие
технические трудности, как в примере с модальными высказываниями.
В результате было построено несколько самостоятельных систем М. л. со своей аксиоматикой, своими законами, отличающимися от законов двузначной логики. Мы не будем вдаваться в суть этих законов — важно, что они построены и что мы поняли, чему они служат.
| Лит.: | Вригт Г. Х. фон. Логика истины // Вригт Г.
Х. фон. Логико-философские исследования. — М., 1986.
Зиновьев А А Философские проблемы многозначной логики — М., 1960. |
| В.Руднев «Словарь
культуры ХХ в.» Многозначные логики |